بحث عن الدائرة ومحيطها

تعريف الدّائرة وخصائصها

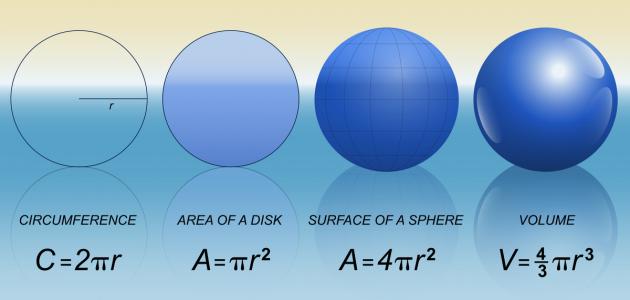
يمكن تعريف الدّائرة (بالإنجليزية: Circle) بأنها عبارة عن مجموعة من النِّقاط المرسومة على سطح مُعيَّن، وتبعُد جميعها المسافة نفسها عن نُقطة معيّنة تُسمّى المركز، في حين تُسمّى المسافة بين أيٍّ من هذه النّقاط ومركز الدّائرة بنصف قُطر الدّائرة (بالإنجليزية: Radius) الذي يُرمز له بالرمز (نق)، أما القُطر (بالإنجليزية: Diameter) فهو يمثّل ضعف هذه المسافة، ويُرمز له بالرمز (ق)،^[١] وعند قسمة محيط أي دائرة على قطرها فإن الناتج يساوي دائماً قيمة ثابتة هي: 3.141592654، والتي تُعرف باسم الثابت باي (بالإنجليزية: Pi)، ورمزه هو (π)،^[٢] ومن خصائص الدائرة ما يأتي:^[٣]

• تتطابق الدائرتان عندما يتساوى طول نصف أقطارهما.
• القطر هو أطول وتر في الدائرة.
• إذا كان نصف القطر عمودياً على الوتر فإنه يقسمه إلى نصفين متساويين.
• إذا تساوى الوتران في بعدهما عن المركز فإنهما يعتبران متساويين في الطول.
• إذا تلاقى المماسان مع الدائرة عند نهايتي القطر فإنهما يعتبران متوازيين.
• تتساوي الأوتار المتطابقة في بعدها عن المركز.^[٤]

لمزيد من المعلومات حول خصائص الدائرة يمكنك قراءة المقال الآتي: خصائص الدائرة.
لمزيد من المعلومات حول قطر الدائرة يمكنك قراءة المقالات الآتية: كيفية حساب قطر الدائرة، ما هو قانون نصف قطر الدائرة.

أجزاء الدائرة ومصطلحاتها

من المصطلحات المتعلقة بالدائرة ما يأتي:^[٥][٦]

• القوس: (بالإنجليزية: Arc) هو أيّ جُزء من محيط الدّائرة.
• القِطاع: (بالإنجليزية: Sector) هي المنطقة المحصورة بين نصفَي قُطرَين مُختلفَين في الدّائرة، وللقطاع الدائري نوعان خاصان هما:
  • الربع الدائري: (بالإنجليزية: Quadrant)، وهو القطاع الدائري الذي تعادل مساحته ربع مساحة الدائرة.
  • نصف الدائرة: (بالإنجليزية: Semicircle)، وهو القطاع الدائري الذي تعادل مساحته نصف مساحة الدائرة.
• الوتر: (بالإنجليزية: Chord) هو خطٍّ مُستقيم يصل بين نقطتَين على محيط الدّائرة.
• القطعة: (بالإنجليزية: Segment) هي المنطقة المحصورة بين أيّ وتر في الدّائرة ومُحيطها.
• محيط الدائرة (بالإنجليزية: Circumference): هو يمثل مسافة الحدود الخارجية للدائرة.
• نصف القطر (بالإنجليزية: Radius): هو يمثل الخط المستقيم الواصل بين مركز الدائرة، وأية نقطة أخرى تقع على محيطها.
• القطر (بالإنجليزية: Diameter): هو عبارة عن وتر يمر بمركز الدائرة، وطوله يساوي القطر=(2× طول نصف القطر).
• المماس: (بالإنجليزية: Tangent) هو عبارة عن خط مستقيم يقع خارج الدائرة بحيث يمس الدائرة عند نقطة واحدة فقط.
• القاطع (بالإنجليزية: Secant): وهو خط مستقيم يقطع الدائرة عبر نقطتين تقعان على محيطها.

مساحة الدّائرة

قانون حساب مساحة الدّائرة

مساحة الدارة هي المنطقة المحصورة داخل حدودها،^[٧] ويمكن حسابها باستخدام أحد القوانين الآتية:^[٨]

• مساحة الدّائرة=π×مربع نصف القطر، وبالرموز: م=π×نق².
• مساحة الدّائرة=(π/4)×مربع القطر، وبالرموز: م=(π/4)×ق².
• مساحة الدّائرة=مربع محيط الدائرة/(π×4)، وبالرموز: م=ح²/(π4).

أمثلة على حساب مساحة الدّائرة

• المثال الأول دائرة نصف قطرها 3سم، جد مساحتها.^[٢]
  • الحلّ: بتعويض قيمة نصف القطر في قانون مساحة الدّائرة، فإنَّ الناتج يكون كما يأتي:
  • م=π×نق²، ومنه م=3.14×3² =28.26سم

• المثال الثاني:دائرة قطرها 10سم، جد مساحتها.^[٧]
  • الحلّ:
  • باستخدام القانون: م=(π/4)×ق²، ينتج أن م=(3.14/4)×10²=78.5سم²

لمزيد من المعلومات والأمثلة حول مساحة الدائرة يمكنك قراءة المقالات الآتية: كيف أحسب مساحة الدائرة، قانون مساحة نصف الدائرة.
لمزيد من المعلومات والأمثلة حول محيط ومساحة الدائرة يمكنك قراءة المقال الآتي: قانون محيط الدائرة ومساحتها.

محيط الدّائرة

قانون محيط الدّائرة

يمكن تعريف محيط الدائرة بأنه طول حدودها الخارجية، ويمكن حسابه باستخدام القوانين الآتية:^[٧][٩]

• محيط الدائرة=2×π×نصف قطر الدائرة، وبالرموز: ح=2×π×نق.
• محيط الدائرة=π×قطر الدائرة، وبالرموز: ح=π×ق.
• محيط الدائرة=الجذر التربيعي للقيمة (4×π×مساحة الدائرة)، وبالرموز: ح=(4×π×م)√.

أمثلة على حساب محيط الدّائرة

• المثال الأول: دائرة نصف قطرها 7سم، جد محيطها.^[٧]
  • الحلّ: بتعويض قيمة نصف القطر في قانون محيط الدّائرة، فإنَّ الناتج يكون كما يأتي:
  • ح=2×π×نق، ومنه م=2×3.14×7=43.96سم.

• المثال الثاني: دائرة قطرها 10سم، جد محيطها.^[٧]
  • الحلّ: بتعويض قيمة القطر في قانون محيط الدّائرة، فإنَّ الناتج يكون كما يأتي:
  • ح=π×ق، ومنه م=3.14×10=31.4سم.

• المثال الثالث: إذا كانت مساحة الدائرة تساوي 81πم²، جد محيطها.^[١٠]
  • الحلّ: باستخدام القانون: محيط الدائرة=الجذر التربيعي للقيمة (4×π×مساحة الدائرة)، ينتج أن: ح=الجذر التربيعي للقيمة (4×π²×81)، ومنه: ح=π18م.

لمزيد من المعلومات والأمثلة حول محيط الدائرة يمكنك قراءة المقالات الآتية: ما هو قانون محيط الدائرة، قانون محيط نصف الدائرة، قانون محيط ربع الدائرة.

معادلة الدّائرة

الصورة العامة لمعادلة الدائرة

يمكن اشتقاق معادلة الدّائرة عن طريق رسم مُثلَّثٍ قائم الزّاوية وتره مُمتَدّ من مركز الدّائرة إلى أيّة نقطة على محيطها، ثُمَّ إكمال رسم الضلعين الآخرين عن طريق رسم الضلع الأول الذي يتمثل بعمود ساقط من نقطة تقاطع الوتر مع محيط الدائرة، ورسم الضلع الآخر ليكون أفقياً ويمتد من مركز الدائرة نحو الضلع العمودي حتى يتلاقى معه، ثم استخدام قانون فيثاغورس وتطبيقه عليه، وفق الحالتين الآتيتين:^[١١]

• معادلة الدائرة المركزية: لو كانت هناك دائرة مركزيّة؛ أي أن مركزها هو النقطة (0،0)، ورُسِم مُثلّث قائم الزّاوية في داخلَها، فيُمكن الإشارة إلى طول قاعدة المُثلَّث القائم المرسوم داخلها بالرّمز (س)، والارتفاع بالرّمز (ص)، وكما ذُكر سابقاً فإن طول الوتر فيها مساوٍ لطول نصف قطرها، وعليه إنَّ معادلة هذه الدائرة ستكون عن طريق تطبيق قانون فيثاغورس على المثلث قائم الزاوية كما يأتي:
  • معادلة الدائرة المركزية: س²+ص²=نصف القطر².

فمثلاً لو كانت هناك دائرة مركزية نصف قطرها 5سم، فإن معادلتها ستكون: س²+ص²=25، ولو كانت قيمة س فيها تساوي 2 فإن قيمة ص هي: 2²+ص²=25، وبحل المعادلة ينتج أن ص=21√.^[١١]

• معادلة الدائرة غير المركزية: أما إذا كانت الدائرة غير مركزيّةً؛ أي أنَّ مركزها لا يقع على النقطة (0،0)؛ فإن طول قاعدة المُثلَّث القائم هو الرمز (س) مطروحاً منه الإحداثي السينيّ لمركز هذه الدائرة، أمّا ارتفاع هذا المثلَّث فيُرمَز له بالرمز (ص) مطروحاً منه الإحداثيّ الصاديّ لمركز الدائرة، وبذلك يمكن اشتقاق معادلةٍ عامة لأية دائرة سواء أكانت دائرة مركزية أم غير مركزية، وهي:^[١١]
• معادلة الدائرة (الصورة القياسية): (س-أ)²+(ص-ب)²=(نصف القطر)²؛ حيث إنَّ:
  • أ: الإحداثيّ السينيّ لمركز الدّائرة.
  • ب: الإحداثيّ الصاديّ لمركز الدّائرة.

وبإعادة ترتيب المعادلة السابقة وتجميع الثوابت مع بعضها، تظهر الصورة العامة لمعادلة الدائرة وهي:

• معادلة الدائرة (الصورة العامة): س²+ص²+دس+و ص+ج=0؛ حيث إنَّ:
  • د=-2×الإحداثيّ السينيّ لمركز الدّائرة.
  • و=-2×الإحداثيّ الصادي لمركز الدّائرة.
  • ج=الإحداثيّ السينيّ لمركز الدّائرة²+الإحداثيّ الصادي لمركز الدّائرة²-نصف قطر الدائرة².

فمثلاً لو كانت هناك دائرة نصف قطرها 6سم، ومركزها هو النقطة (3,4) فإن معادلتها ستكون: (س-3)²+(ص-4)²=36، وبفك الأقواس يمكن الحصول على الصورة العامة لمعادلة الدائرة، وهي: س²+ص²-6س-8ص-11=0، ولو كانت قيمة س مثلاً تساوي 3 فإن قيمة ص هي: (3-3)²+(ص-4)²=36، وبحل المعادلة ينتج أن ص=10، -2.^[١١]

أمثلة متنوعة على معادلة الدائرة

• المثال الأول: إذا كانت الصورة القياسية لمعادلة الدائرة هي: (س+11)²+(ص-9)²=16، جد الصورة العامة لها.^[١١]
  • الحل: بفك الأقواس ينتج أن: (س+11)²+(ص-9)²=16=س²+22س+121+ص²-18ص+81=16، وبتبسيط المعادلة ينتج أن: س²+ص²-18ص+22س+186=0.

• المثال الثاني: جد معادلة الدائرة المركزية التي يبلغ نصف قطرها 4.^[١١]
  • الحل: باستخدام الصورة القياسية لمعادلة الدائرة المركزية: س²+ص²=(نصف القطر)²، ينتج أن: س²+ص²=4²، ومنه س²+ص²=16.

• المثال الثالث: جد معادلة الدائرة إذا كان مركزها (3،-5)، وتقع النقطة (-1،-8) على محيطها.^[١١]
  • الحل:
  • استخدام الصورة القياسية لمعادلة الدائرة: (س-أ)²+(ص-ب)²=(نصف القطر)²، لينتج أن: (س-3)²+(ص+5)²=(نصف القطر)².
  • تعويض قيمة النقطة (-1،-8) في المعادلة السابقة لحساب قياس نصف القطر، لينتج أن: (-1-3)²+(-8+5)²=(نصف القطر)²، ومنه نصف القطر=5.
  • تعويض قيمة نصف القطر في المعادلة لتصبح: (س-3)²+(ص+5)²=(نصف القطر)²، (س-3)²+(ص+5)²=25، وهي الصورة القياسية لمعادلة الدائرة، ويمكن تفكيك الأقواس وتبسيط المعادلة لتصبح: س²+ص²-6س+10ص+9=0

قوانين متنوعة متعلقة بالدائرة

من القوانين المتعلقة بالدائرة ما يأتي:

• قانون حساب طول وتر الدائرة: يمكن حساب طول وتر الدائرة من خلال إحدى الصيغ الآتية:^[٩]
  • طول الوتر=2×نصف قطر الدائرة×جا(الزاوية المركزية/2).
  • طول الوتر=2×نصف قطر الدائرة×جا(الزاوية المحيطية)؛ حيث:
    • الزاوية المركزية (بالإنجليزية: central angle): هي الزاوية التي يقع رأسها على مركز الدائرة، وفي هذه الحالة هي الزاوية المحصورة بين نصفي القطر، والمقابلة للوتر الواصل بينهما، وهو المطلوب حساب طوله.
    • الزاوية المحيطية (بالإنجليزية: Inscribed angle): هي الزاوية التي يقع رأسها على محيط الدائرة، وفي هذه الحالة هي الزاوية المحصورة بين الوترين اللذين يصل الوتر المطلوب حساب طوله بينهما.
• قانون حساب مساحة القطاع الدائري: يمكن حساب مساحة القطاع الدائري من خلال الصيغة الآتية:^[٩]
• مساحة القطاع الدائري=(π×مربع نصف القطر/360)×قياس زاويته المركزية، وبالرموز:
• مساحة القطاع الدائري=(π×نق² /360)×α؛ حيث:
  • نق: نصف قطر الدائرة.
  • α: قياس الزاوية المركزية للقطاع الدائري.
• قانون حساب طول القوس الدائري: يمكن حساب طول القوس الدائري من خلال الصيغة الآتية:^[٩]
• مساحة القطاع الدائري=(π×نصف القطر/180)×قياس الزاوية المركزية المقابلة للقوس، وبالرموز:
• طول القوس الدائري=(π×نق /180)×α؛ حيث:
  • نق: نصف قطر الدائرة.
  • α: قياس الزاوية المركزية المقابلة للقوس.

أمثلة على حساب القطاع وقوس الدائرة

• المثال الأول: إذا كان نصف قطر الدائرة يساوي 8م، وقياس الزاوية المركزية للقطاع 45 درجة، جد مساحة القطاع الدائري، وطول القوس.^[١٢]
  • الحل:
  • باستخدام القانون مساحة القطاع الدائري=(π×نق² /360)×α، ينتج أن: مساحة القطاع الدائري= (π ×8² /360)×45، ومنه مساحة القطاع الدائري=π8.
  • باستخدام القانون: طول القوس الدائري=(π×نق /180)×α ينتج أن طول القوس=(π×8 /180)×45، ومنه طول القوس الدائري= 2π.

• المثال الثاني: إذا كان طول القوس المقابل للقطاع الدائري 12سم، وكانت مساحة هذا القطاع 108سم²، جد قطر هذه الدائرة.^[١٢]
  • الحل:
  • باستخدام القانون مساحة القطاع الدائري=(π×نق² /360)×α، ومنه 108=(π×نق² /360)×α.
  • وباستخدام القانون طول القوس الدائري=(π×نق /180)×α، ومنه 12=(π×نق /180)×α.
• وبحل المعادلتين السابقتين ينتج أن: نق=18سم، وعليه فإن قطر الدائرة=2×نصف القطر=2×18=36سم.

لمزيد من المعلومات والأمثلة حول مساحة القطاع الدائري يمكنك قراءة المقال الآتي: قانون مساحة القطاع الدائري.
لمزيد من المعلومات والأمثلة حول طول قوس الدائرة يمكنك قراءة المقال الآتي: قانون طول قوس الدائرة.

كيفيّة رسم الدّائرة

يُستخدَم الفرجار عادةً لرسم دائرة مُتقَنة على سطح ما، والفرجار هو عبارة عن أداة تتكوَّن من ذراعَين معلّقتَين معاً ومُتحرّكتَين؛ ويكون لدى إحداهما رأس مُدبَّب، أمَّا الذّراع الأخرى فيُثبَّت فيها قلم رصاص، ويُمكن استخدام الفرجار أيضاً لرسم أجزاء من الدّائرة، ولرسم الدائرة باستخدام الفرجار يجب اتّباع الخطوات الآتية:^[٦]

• التأكُّد من أنَّ رأس الفرجار ثابتة؛ حتّى لا ينزلق الفرجار أثناء استخدامه.
• شدّ البُرغي المُثبِّت للقلم؛ حتى لا ينزلق القلم أثناء الرّسم.
• جعل رأس القلم بنفس مُستوى الذّراع الأخرى للفرجار.
• تثبيت الرأس المُدبَّب للفرجار على السَّطح المُراد الرّسم عليه، ومن ثُمَّ تحريك الفرجار بشكل دائريّ حول رأسه؛ لرسم دائرة أو جزءٍ منها.
• في حال التقيُّد بنصف قُطر مُعيَّن للدّائرة، فيجب جينها استخدام المسطرة لتحديد قيمة فتحة الفرجار؛ حتّى تصبح بنفس طول نصف القطر المطلوب، ومن ثُمَّ يُثبّت الفرجار على السطح، وتُرسَم الدّائرة.

المراجع

1. ↑ “Circle”, Wolfram Mathworld, Retrieved 10-3-2017. Edited.
2. ^ ^{أ ب} “Circle”, www.mathsisfun.com, Retrieved 10-3-2020. Edited.
3. ↑ “Properties of Circle”, byjus.com, Retrieved 11-3-2020. Edited.
4. ↑ “Circle Geometry Properties”, brilliant.org, Retrieved 11-3-2020. Edited.
5. ↑ Richard Elwes‏، (فكرة 1001 عن الرياضيات (الأعداد-الهندسة-الجبر-علم الإحصاء، صفحة: 147-149.
6. ^ ^{أ ب} “Circles and using a Compass “, mathsteacher.com.au, Retrieved 10-3-2017. Edited.
7. ^ ^{أ ب ت ث ج} “Area of a Circle”, byjus.com, Retrieved 11-3-2020. Edited.
8. ↑ “Area of a Circle”, www.mathsisfun.com, Retrieved 11-3-2020. Edited.
9. ^ ^{أ ب ت ث} “Circle, disk, segment, sector. Formulas, characterizations and properties of circle”, onlinemschool.com, Retrieved 11-3-2020. Edited.
10. ↑ “Example Questions”, www.varsitytutors.com, Retrieved 11-3-2020. Edited.
11. ^ ^{أ ب ت ث ج ح خ} “Circle Equations”, www.mathsisfun.com, Retrieved 10-3-2017. Edited.
12. ^ ^{أ ب} “Sectors, Areas, and Arcs”, www.purplemath.com, Retrieved 11-3-2020. Edited.