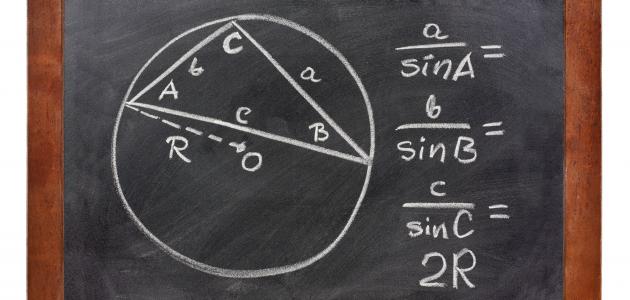نظرة عامة حول قانون الجيب
يمكن تعريف قانون الجيب (بالإنجليزية: Sine Law) في حساب المثلثات على أنَّه علاقة رياضيّة تربط بين أطوال أضلاع أي مثلث بجيوب زواياه الداخلية،[١] وتُستخدم لحساب الأضلاع والزوايا المجهولة في المثلث إذا عُلم طول ضلعين منه وزاوية ليست محصورة بينهما، أو إذا عُلم قياس زاويتين وضلع منه.[٢]
لمزيد من المعلومات حول قانون الجيب وجيب التمام يمكنك قراءة المقال الآتي: قانون الجيب وقانون جيب التمام.
صيغة قانون الجيب
يعبّر عن قانون الجيب في الرياضيات وفقاً للعلاقة الرياضية الآتية:[١]
- (أ/جا أَ)=(ب/جا بَ)=(جـ/جا جـَ) حيث إنَّ:
- (أ، ب، ج) هي أطوال أضلاع المثلث، و(أَ، بَ، جَ) هي الزوايا المقابلة على الترتيب لهذه الأضلاع.
- كما يُمكن كذلك كتابة قانون الجيب في الرياضيات على الصورة الآتية: (جا أَ/أ)=(جا بَ/ب)=(جا جـَ/جـَ).
لمزيد من المعلومات حول قانون جيب التمام يمكنك قراءة المقال الآتي: ما هو قانون جيب التمام.
أمثلة على قانون الجيب
- المثال الأول: احسب طول الضلع أ، إذا كان قياس الزاوية أَ=82 درجة، والزاوية بَ=20 درجة، وطول الضلع ب= 6 وحدات.[٣]
- الحل:
- باستخدام قانون الجيب: أ/جا أَ=ب/جابَ=ج/جا جَ، ينتج أن:
- أ/جا(82)=6/جا(20)=أ/0.99=6/ 0.34، ومنه ينتج أ=18 وحدة تقريباً.
- المثال الثاني: احسب قياس الزاوية بَ، إذا كان طول الضلع أ=10، وطول الضلع ب=9، وقياس الزاوية أَ=26 درجة.[٤]
- الحل:
- باستخدام قانون الجيب: أ/جا أَ=ب/جابَ=ج/جا جَ، ينتج أن:
- 10/جا(26)=9/جا(بَ)، ومنه ينتج جا(بَ)= 9/10*جا(26)، ومنه بَ=23.237° تقريباً، ولأن جا س=جا(180-س) فإنه يمكن لهذا السؤال أن تكون قيمة الزاوية فيه أيضاً: 180-23.24=156.763° درجة.
- المثال الثالث: إذا كان قياس الزاوية ق في المثلث (ق رب)= 39°، وطول الضلع ق ب=41سم، والضلع ب ر=28سم، جد قياس الزاوية ر.[١]
- الحل:
- باستخدام قانون الجيب: أ/جا أَ=ب/جابَ=ج/جا جَ، ينتج أن:
- 41/جا(ر)=28/جا(39)، ومنه جا(ر)=0.92، وقياس الزاوية (ر)=67.1°ولأن جا س=جا(180-س) فإنه يمكن لهذا السؤال أن تكون قيمة الزاوية فيه أيضاً: 180-67.1=112.9°.
- المثال الرابع: إذا كان قياس الزاوية ب في المثلث (أب جـ) 32°، وكان قياس الزاوية أ=69°، وطول أب=5.7سم، جد طول أجـ.[٥]
- الحل:
- حساب قياس الزاوية الثالثة في المثلث من خلال حقيقة أن مجموع زوايا المثلث يساوي 180°، لينتج أن قياس الزاوية جـ=180-(32+69)= 79°، وباستخدام قانون الجيب: أ/جا أَ=ب/جابَ=ج/جا جَ، ينتج أن:
- أجـ/جا(32)=5.7/جا(79)، ومنه أجـ=3.08سم.
- المثال الخامس: إذا كان قياس الزاوية ب في المثلث (أب جـ) 108°، وكان قياس الضلع أجـ=11.7سم، وطول أب=5.6سم، جد طول ب جـ.[٥]
- الحل:
- لحساب طول الضلع (ب جـ) يجب إيجاد قياس الزاوية المقابلة له، وهي الزاوية أ، وذلك باستخدام قانون الجيب أولاً، ثم حقيقة أن مجموع زوايا المثلث=180° ثانياً، وذلك كما يلي:
- باستخدام قانون الجيب: أ/جا أَ=ب/جابَ=ج/جا جَ، ينتج أن: أجـ/جا(ب)=أب/جا(جـ)=ب جـ/جا(أ)، وبتعويض القيم فيها ينتج أن:
- 11.7/جا(108)=5.6/جا(جـ)، ومنه جـ=27.08°، ثم حساب قيمة الزاوية (أ): 180-(27.08+108)=44.9°.
- تعويض القيم في قانون الجيب: أجـ/جا(ب)=ب جـ/جا(أ)، لينتج أن: 11.7/جا(108)=ب جـ/جا (44.9)، ومنه ب جـ= 8.68سم.
- المثال السادس: إذا كان لدى قصي حقل مثلث الشكل طول أحد أضلاعه 300م، وقياس الزاوية المقابلة لهذا الضلع 27°، والزاوية المجاورة لها 114°، جد عدد الأمتار التي سيحتاجها قصي لتسييج حقله بالكامل.[٥]
- الحل:
- يجب لحساب عدد الأمتار المطلوبة لتسييج الحقل حساب محيطه أولاً، والذي يتم عن طريق حساب جميع أضلاع هذا المثلث كما يأتي:
- نفترض أن الحقل هو المثلث (أب جـ)، فيه الزاوية جـ=114°، والزاوية ب=27°، والضلع أجـ=300م، أما الزاوية أ فهي 180-(114+27)= 39°.
- باستخدام قانون الجيب أجـ/جا(ب)=أب/جا(جـ)=ب جـ/جا(أ)، ينتج أن: 300/جا (27)=أب/جا (114)=ب جـ/جا (39)، وبأخذ الجزء الأول 300/جا (27)=أب/جا (114) ينتج أن: أب=603.7م، وبأخذ الجزء الثاني: 603.7/جا (114)=ب جـ/جا (39) ينتج أن: ب جـ=415.67م.
- حساب محيط المثلث الذي يساوي مجموع أطوال أضلاعه، لينتج أن: عدد الأمتار المطلوبة لتسييج الحقل=415.67+603.7+300 =1320م.
- المثال السابع: إذا كان قياس الزاوية ب في المثلث (أب جـ)= 21°، وكان طول أب=9سم، وقياس الزاوية جـ=46°، جد طول جميع أضلاع وزايا هذا المثلث.[٦]
- الحل:
- حساب قياس الزاوية أ عن طريق معرفة أن مجموع زوايا المثلث=180°، ومنه: أ=180-(46+21)=113°.
- باستخدام قانون الجيب أجـ/جا(ب)=أب/جا(جـ)=ب جـ/جا(أ)، وتعويض القيم فيه ينتج أن:
- أجـ/جا(21)=9/جا(46)، ومنه طول الضلع أجـ= 4.48سم.
- 9/جا(46)=ب جـ/جا(113)، ومنه: ب جـ= 11.52سم.
- المثال الثامن: إذا كان هناك جدار بطول 1.4م، بدأ بالميلان نحو الأرض حتى أصبحت الزاوية المتشكّلة بينه وبين الأرض 80° تماماً، فإذا تم إسناده بواسطة لوح طوله 2م بشكل مائل، ويمتد من نهاية الجدار وحتى نقطة على الأرض تبعد مسافة (ف) عن أسفل الجدار، جد الزاوية المحصورة بين اللوح والأرض، والمسافة الممتدة من أسفل الجدار، وحتى أسفل اللوح.[٢]
- الحل:
- تبيّن بعد تمثيل السؤال أن الجدار واللوح يشكّلان مع الأرض مثلثاً أطوال أضلاعه كالآتي:
- الضلع الأول وطوله 2م، هو اللوح الممتد من الأرض حتى أعلى الجدار.
- الضلع الثاني وهو الجدار، وطوله 1.4م.
- الضلع الثالث وهو المسافة بين أسفل الجدار، وأسفل اللوح وطولها (ف).
- لحساب الزاوية المحصورة بين اللوح والأرض (س)، يمكن استخدام قانون الجيب: أ/جا أَ=ب/جابَ=ج/جا جَ ، لينتج أن: 1.4/جا(س)=2/جا(80)، ومنه س=43.6°، وهي الزاوية المحصورة بين اللوح والأرض.
- لحساب المسافة (ف) بين أسفل الجدار، وأسفل اللوح، يمكن استخدام قانون الجيب مرة أخرى كالآتي: ف/جا(فَ)=2/جا(80)، ولحساب قيمة فَ يمكن الاستعانة بخاصية أن مجموع زوايا المثلث=180°، ومنه: فَ=180-(80+43.6)=56.4°، وبتعويض قيمتها في القانون السابق ينتج أن: ف=1.69م.
- المثال التاسع: إذا كان قياس الزاوية أ في المثلث (أب جـ) 30°، وكان قياس الضلع ب جـ=6سم، وطول أب=10سم، جد أكبر قياس ممكن لإحدى زواياه.[٧]
- الحل:
- باستخدام قانون الجيب أجـ/جا(ب)=أب/جا(جـ)=ب جـ/جا(أ) وتعويض القيم فيه، ينتج أن:
- 6/جا(30)=10/جا(جـ)، وبحل مما سبق، ينتج أن: جـ=56.44°، أو جـ=180-56.44=123.55°؛ لأن جيب الزاوية يساوي جيب الزاوية المكمّلة لها.
- حساب قياس الزاوية الثالثة، وهي الزاوية ب من خلال خاصية أن مجموع زوايا المثلث=180°، وبالتالي قياس (ب)=180-(56.44+30)=93.56°، إذا كانت جـ=56.44°، أو قياس (ب)=180-(123.55+30)=26.45°، إذا كانت جـ=123.55°.
- القياسات الممكنة لزوايا هذا المثلث هي: 30°، 56.44°، 93.56°، أو 30°، 26.45°، 123.55°، ومما سبق ينتج أن أكبر قياس ممكن لإحدى زوايا هذا المثلث هو: 123.55°.
المراجع
- ^ أ ب ت “The Law of Sines”, www.mathsisfun.com, Retrieved 24-6-2018. Edited.
- ^ أ ب “Applications of the Sine Law”, www.highskills.ca, Retrieved 7-4-2020. Edited.
- ↑ Jeff Calareso، “Law of Sines: Definition and Application”، www.study.com، Retrieved 22-11-2017. Edited.
- ↑ Pi Han Goh, Edward Tsoi, Worranat Pakornrat,, “Sine Rule (Law of Sines)”، brilliant.org, Retrieved 7-4-2020. Edited.
- ^ أ ب ت “The Law of Sines “, www.mathopolis.com, Retrieved 7-4-2020. Edited.
- ↑ “The sine rule and cosine rule”, www.mathcentre.ac.uk, Retrieved 7-4-2020. Edited.
- ↑ “Law of Sines”, www.varsitytutors.com, Retrieved 7-4-2020. Edited.