محتويات
مساحة شبه المنحرف القائم
يمثّل شبه المنحرف القائم (بالإنجليزية: Right Trapezoid) حالة خاصة أو نوعاً من أنواع شبه المنحرف، وهو يتميز بامتلاكه لزاويتين قائمتين متجاورتين،[١] ويمكن حساب مساحته باستخدام القانون العام لحساب مساحة شبه المنحرف، وهو:[٢]
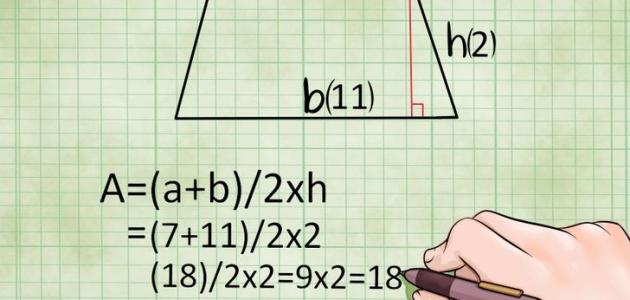
- مساحة شبه المنحرف= ½×(مجموع القاعدتين)×الارتفاع، وبالرموز:
- م= ½×(ق1+ق2)×ع؛ حيث:
- م: مساحة شبه المنحرف.
- ق1، ق2: طول قاعدتي شبه المنحرف.
- ع: ارتفاع شبه المنحرف.
لمزيد من المعلومات والامثلة حول مساحة شبه المنحرف يمكنك قراءة المقال الآتي: مساحة الشبه المنحرف.
لمزيد من المعلومات والامثلة حول شبه المنحرف يمكنك قراءة المقال الآتي: بحث عن شبه المنحرف.
لمزيد من المعلومات والامثلة حول خصائص شبه المنحرف يمكنك قراءة المقال الآتي: خصائص الشبه منحرف.
أمثلة متنوعة حول مساحة شبه المنحرف القائم
المثال الأول
- إذا كانت لدى أحمد حديقة على شكل شبه منحرف قائم، يبلغ ارتفاعها 3.4م، وطول قاعدتها السفلية 8.2م، والعلوية 5.6م، جد المساحة المتاحة للزراعة في هذه الحديقة.[٣]
- الحل:
- بتطبيق قانون مساحة شبه المنحرف: ½×(مجموع القاعدتين)×الارتفاع=½×(8.2+5.6)×3.4=23.46م²، وهي المساحة المتاحة للزراعة في هذه الحديقة.
- الحل:
المثال الثاني
- جد مساحة شبه المنحرف القائم الذي يبلغ طول قاعدته السفلية 10سم، وقاعدته العلوية 6سم، وارتفاعه 8سم.[٤]
- الحل: بتطبيق قانون حساب مساحة شبه المنحرف: ½×(مجموع القاعدتين)×الارتفاع= ½×(10+6)×8=64سم².
المثال الثالث
- جد مساحة شبه المنحرف القائم الذي يبلغ طول قاعدته السفلية 52سم، وقاعدته العلوية 28سم، وساقه الجانبية غير القائمة على القاعدتين 40سم.[٤]
- الحل:
- حساب الارتفاع بتطبيق قانون فيثاغورس؛ حيث (طول الساق الجانبية غير القائمة على القاعدتين)²=(طول القاعدة السفلية-طول القاعدة العلوية)²+(طول الساق القائمة على القاعدتين)²=(40)²=(52-28)²+(الارتفاع)²، ومنه: الارتفاع=32سم.
- تطبيق قانون حساب مساحة شبه المنحرف: ½×(مجموع القاعدتين)×الارتفاع= ½×(52+28)×32=1,280سم².
- الحل:
المثال الرابع
- جد مساحة شبه المنحرف القائم الذي يبلغ طول قاعدته السفلية 11.6سم، وقاعدته العلوية 6.4سم، وارتفاعه 5سم.[٥]
- الحل: بتطبيق قانون حساب مساحة شبه المنحرف: ½×(مجموع القاعدتين)×الارتفاع= ½×(11.6+6.4)×5=45سم².
المثال الخامس
- جد مساحة شبه المنحرف القائم الذي يبلغ طول قاعدته السفلية 8سم، وقاعدته العلوية 5سم، وارتفاعه 4سم.[٦]
- الحل: بتطبيق قانون حساب محيط شبه المنحرف: م= ½×(مجموع القاعدتين)×الارتفاع= ½×(5+8)×4=26سم².
المثال السادس
- جد طول القاعدة السفلية لشبه المنحرف (أب ج د) القائم في (ب)و(ج)، الذي يبلغ طول قاعدته العلوية (أب) 15سم، وارتفاعه (أو) 12سم، ومساحته 198سم².[٤]
- الحل: بتطبيق قانون حساب محيط شبه المنحرف: م= ½×(مجموع القاعدتين)×الارتفاع، ينتج أن 198=½×(15+ق2)×12، ومنه ق2=18سم.
لمزيد من المعلومات والامثلة حول ارتفاع شبه المنحرف يمكنك قراءة المقال الآتي: ارتفاع شبه المنحرف.
لمزيد من المعلومات والامثلة حول قوانين شبه المنحرف يمكنك قراءة المقال الآتي: قوانين شبه المنحرف.
فيديو عن شبه المنحرف خصائصه ومساحته
للتعرف حول المزيد شاهد الفيديو:[٧]
المراجع
- ↑ “Trapezoid: Definition, Properties & Formulas”, study.com, Retrieved 26-2-2020. Edited.
- ↑ “Right Trapezoid”, mathworld.wolfram.com, Retrieved 26-2-2020. Edited.
- ↑ “9.7: Use Properties of Rectangles, Triangles, and Trapezoids (Part 2)”, math.libretexts.org, Retrieved 26-2-2020. Edited.
- ^ أ ب ت “Area of Trapezoids”, www.murrieta.k12.ca.us, Retrieved 26-2-2020. Edited.
- ↑ “TRAPEZOIDS”, www.cbsd.org, Retrieved 26-2-2020. Edited.
- ↑ “Area of Trapezoid”, www.softschools.com, Retrieved 26-2-2020. Edited.
- ↑ فيديوعن شبه المنحرف خصائصه ومساحته.