محتويات
يمكن تعريف الانحراف المعياري (بالإنجليزية: Standard Deviation) بأنه مقدار بُعد البيانات وانتشارها بالنسبة للوسط الحسابي، أما رمز الانحراف المعياري فهو الرمز (σ)،[١] ويمكن إيجاده عن طريق حساب الجذر التربيعي للتباين،[٢] ويختلف الانحراف المعياري عن التباين من ناحية أن الانحراف المعياري يقيس تشتت البيانات ومقدار اختلافها عن المتوسط الحسابي، أما التباين فيصف اختلافها، ويحدد مقدار انتشار البيانات وبعدها عن بعضها البعض وعن المتوسط الحسابي.[٣]
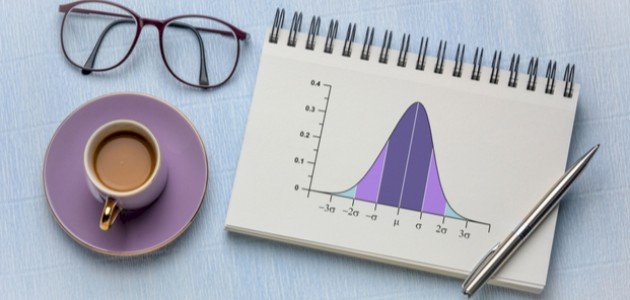
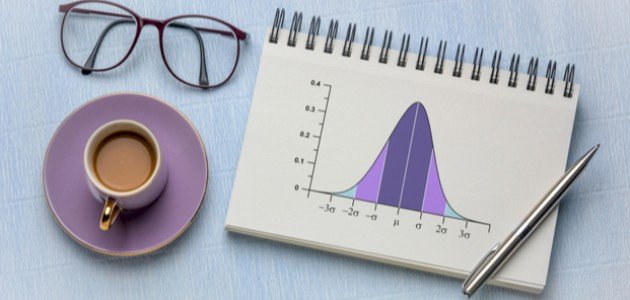
يتم تحديد كل من المتوسط الحسابي والانحراف المعياري معاً شكل المنحنى الطبيعي لمجموعة البيانات؛ فالمتوسط الحسابي يحدد مركز هذه البيانات أو منتصفها، ومقدار ارتفاع المنحنى الطبيعي، أما الانحراف المعياري فيحدد مقدار عرض ذلك المنحنى،[٤] ويجدر بالذكر أنه كلما اقترب الانحراف المعياري من القيمة (0)، فذلك يعني أن القيم الموجودة أكثر قرباً للمتوسط الحسابي، وفي المقابل تُشير القيم الكبيرة من الانحراف المعياري إلى بعد القيم عن المتوسط الحسابي.[٥] يجدر بالذكر هنا أن هناك نوعين من الانحراف المعياري، هما:[٦]
(بالإنجليزية: Sample Standard Deviation) ويُرمز له بالرمز (S)، ويستخدم إذا كانت البيانات المستخدمة في حساب الانحراف المعياري لا تمثّل كامل البيانات في المجتمع أو الدراسة، وإنما عينة منها، بسبب كثرة عدد أفراد أو أعضاء الدراسة أو المجتمع، ويُحسب الانحراف المعياري في هذه الحالة باستخدام العلاقة الآتية:
- الانحراف المعياري للعينة = [مجموع (س-الوسط الحسابي للعينة)² / (ن-1)]√، حيث:
- ن: عدد القيم، (ن-1) تعرف بأنها تصحيح بسل (Bessel’s correction).
- س: القيم المشمولة في الدراسة.
(بالإنجليزية: Population Standard Deviation) ويُرمز له بالرمز (σ)، ويُستخدم عند استخدام كافة أفراد المجتمع أو الدراسة كبيانات حساب الانحراف المعياري، وذلك كما في المثال السابق:
- الانحراف المعياري للمجتمع = [مجموع (س-μ)²/ن]√، حيث
- ن: عدد القيم.
- س: القيم المشمولة في الدراسة.
- μ : المتوسط الحسابي للقيم.
يحسب الانحراف المعياري من خلال حساب المتوسط الحسابي، وهو: المتوسط الحسابي= (مركز الفئة×التكرار)/مجموع التكرارات
- حساب الانحراف المعياري للجداول التكرارية = [مجموع (التكرار×(مركز الفئة – المتوسط الحسابي)²)/مجموع التكرارات]√
- الخطوة الأولى هي إيجاد الوسط الحسابي للقيم، وذلك باستخدام القانون الآتي الوسط الحسابي = مجموع القيم/عددها.
- الخطوة الثانية هي طرح الوسط الحسابي من كل قيمة من القيم، وتربيع القيمة الناتجة.
- الخطوة الثالثة هي إيجاد مجموع القيم المربعة السابقة.
- الخطوة الرابعة هي قسمة المجموع السابق على عدد القيم.
- الخطوة الخامسة هي إيجاد الجذر التربيعي لهذه القيمة
يمثل الآتي بعض التمارين على الانحراف المعياري:
- المثال الأول: يوضح حساب الانحراف المعياري للجداول التكرارية:
إذا كان عدد الطلاب اللذين تتراوح علاماتهم بين 4، و8 هو 3 طلاب، وعدد الطلاب الذين تتراوح علاماتهم بين 8، و12 هو 6 طلاب، وعدد الطلاب الذين تتراوح علاماتهم بين 12، و16 هو 4 طلاب، وعدد الطلاب الذين تتراوح علاماتهم بين 16، و20، فما هو الانحراف المعياري لهذه القيم؟[٧]
الحل:
الفئة | مركز الفئة (الحد الأعلى للفئة+الحد الأدنى للفئة)/2 | التكرار |
4-8 | 6 | 3 |
8-12 | 10 | 6 |
12 – 16 | 14 | 4 |
16 – 20 | 18 | 7 |
- لحساب الانحراف المعياري يجب أولاً حساب المتوسط الحسابي، وهو: المتوسط الحسابي= (مركز الفئة×التكرار)/مجموع التكرارات، ويساوي: الوسط الحسابي = (3×6 + 6×10 + 4×14 + 7×18)/ 20 = 13.
- حساب الانحراف المعياري = [مجموع (التكرار×(مركز الفئة – المتوسط الحسابي)²)/مجموع التكرارات]√، وبالتالي:
- الانحراف المعياري = [(3×(6-13)² + 6×(10-13)² + 4×(14-13)² + 7×(18-13)²)/20]√ = [(147+ 54 + 4 + 175)/20 ]√= 19√ = 4.36.
- المثال الثاني: ما هو الانحراف المعياري للقيم الآتية: 6، 2، 3، 1؟[٥]
الحل:
قانون الانحراف المعياري = [مجموع (س-μ)²/ن]√.
الخطوة الأولى هي إيجاد المتوسط الحسابي:
المتوسط الحسابي = مجموع القيم/عددها= (6+2+3+1)/4= 12/4 = 3.
إن أفضل طريقة لإيجاد الانحراف المعياري هي عمل جدول، وتطبيق القانون عليه كما يلي:
القيمة | القيمة – المتوسط الحسابي | ( القيمة – المتوسط الحسابي)² |
6 | 6-3 =3 | 9 |
3 | 3-3 = 0 | 0 |
2 | 2-3 = -1 | 1 |
1 | 1 -3 = -2 | 4 |
المجموع | – | 14 |
وبالتالي فإن الانحراف المعياري = (14/4)√ = 1.87 تقريباً.
- المثال الثالث: ما هو الانحراف المعياري للقيم الآتية التي تمثل عينة من أحد المجتمعات: 4، 6، 2، 2، 1؟[٨]
الحل:
الانحراف المعياري للعينة = [مجموع (س-الوسط الحسابي للعينة)² / (ن-1)]√.
الخطوة الأولى هي إيجاد الوسط الحسابي كما يلي:
المتوسط الحسابي = مجموع القيم/عددها = (6+4+2+2+1)/5 = 15/5 = 3.
إن أفضل طريقة لإيجاد الانحراف المعياري هي عمل جدول، وتطبيق القانون عليه كما يلي:
القيمة | القيمة – المتوسط الحسابي | ( القيمة – المتوسط الحسابي)² |
1 | 1 – 3 =-2 | 4 |
2 | 2 – 3 = -1 | 1 |
2 | 2 – 3 = -1 | 1 |
4 | 4 – 3 = -1 | 1 |
6 | 6 – 3 = 3 | 9 |
المجموع | – | 16 |
وبالتالي فإن الانحراف المعياري= [16/(5-1)]√ =2.
- المثال الرابع: ما هو الانحراف المعياري للقيم الآتية: 4، 9، 11، 12، 17، 5، 8، 12، 14؟[٩]
الحل:
الانحراف المعياري = [مجموع (س-μ)²/ن]√.
الخطوة الأولى هي إيجاد المتوسط الحسابي كما يلي:
المتوسط الحسابي = مجموع القيم/عددها = 4+9+11+12+17+5+8+12+14 = 92/9 = 10.222 تقريباً.
إن أفضل طريقة لإيجاد الانحراف المعياري هي عمل جدول، وتطبيق القانون عليه كما يلي:
القيمة | القيمة – المتوسط الحسابي | ( القيمة – المتوسط الحسابي)² |
4 | 4 – 10.222 = -6.222 | 38.7 |
9 | 9 – 10.222 = -1.222 | 1.49 |
11 | 11 – 10.222 = 0.778 | 0.6 |
12 | 12 – 10.222 = 1.778 | 3.16 |
17 | 17 -10.222 = 6.778 | 45.9 |
5 | 5 – 10.222 = -5.222 | 27.3 |
8 | 8 – 10.222 = -2.222 | 4.94 |
12 | 12 – 10.222 = 1.778 | 3.16 |
14 | 14 – 10.222 = 3.778 | 14.3 |
المجموع | – | 139.55 |
وبالتالي فإن الانحراف المعياري = [139.55/9]√ = 3.94.
- ↑ “Standard Deviation Formulas”, www.mathsisfun.com, Retrieved 27-5-2020. Edited.
- ↑ “Standard Deviation Definition”, www.investopedia.com, Retrieved 27-5-2020. Edited.
- ↑ “Difference Between Variance and Standard Deviation”, keydifferences.com, Retrieved 27-5-2020. Edited.
- ↑ “Here’s What Nerds Mean When They Say ‘Standard Deviation'”, www.businessinsider.com, Retrieved 27-5-2020. Edited.
- ^ أ ب “Calculating standard deviation step by step”, www.khanacademy.org, Retrieved 27-5-2020. Edited.
- ↑ “Standard Deviation Formulas”, www.mathsisfun.com, Retrieved 27-5-2020. Edited.
- ↑ “Measures of dispersion”, ncert.nic.in, Retrieved 27-5-2020. Edited.
- ↑ “How to Calculate a Sample Standard Deviation”, www.thoughtco.com, Retrieved 27-5-2020. Edited.
- ↑ “Standard Deviation”, revisionmaths.com, Retrieved 28-5-2020. Edited.