جديد قانون محيط المعين

قانون محيط المعين

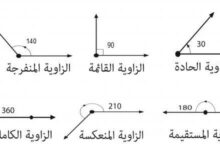
المعين هو شكل مسطح له أربعة أضلاع متساوية، وأربع زوايا لا يُشترط لقياساتها أن تكون 90 درجة، ويعرف محيط المعين (بالإنجليزية: Perimeter of Rhombus) بأنه المسافة الكلية التي تحيط بالشكل الخارجي، وبشكل عام يُعطى محيط المعين بالعلاقات الآتية:^[١]

• حساب محيط المعين باستخدام طول الضلع:
  • محيط المعين = 4 × طول الضلع.
  • وبالرموز ح=4×ل؛ فجميع أضلاع المعين متساوية؛ حيث:
    • ل: طول ضلع المعين.
• حساب محيط المعين باستخدام طول القطرين:
  • محيط المعين =2× ((القطر الأول)²+(القطر الثاني)²)√.
  • وبالرموز: م=2× (ق²+ل²)√؛ حيث:^[٢]
    • ق: طول القطر الأول.
    • ل: طول القطر الثاني.

أمثلة على حساب محيط المعين

حساب محيط المعين من طول الضلع

• المثال الأول: ما هو محيط المعين الذي طول ضلعه 5سم.^[١]
  • الحل: تطبيق قانون محيط المعين = 4× طول الضلع = 4× 5= 20سم.

• المثال الثاني: معين طول أحد أضلاعه 9.5سم، فما هو محيطه؟^[٣]
  • الحل: تطبيق قانون محيط المعين = 4 × طول الضلع= 4 × 9.5= 38سم.

• المثال الثالث: إذا كان محيط المعين 260سم، جد طول ضلعه.^[٢]
  • الحل:
  • بتطبيق قانون: محيط المعين = 4 × طول الضلع، ينتج أن طول الضلع=محيط المعين÷4=4 /260=65سم.

• المثال الرابع: إذا كان محيط المعين 217سم، جد طول ضلعه.^[٤]
  • الحل:
  • بتطبيق قانون: محيط المعين = 4 × طول الضلع، ينتج أن طول الضلع=محيط المعين÷4=4 /217=54.25سم.

حساب محيط المعين من المساحة

• المثال الأول: معين مساحته 42 وحدة مربعة، وارتفاعه يساوي 7، فما هو محيطه.^[٣]
  • الحل:
  • حساب طول الضلع من قانون مساحة المعين = طول القاعدة × الارتفاع، ومنه 42 = طول القاعدة × 7، وبالتالي فإن طول القاعدة يساوي 6سم.
  • تطبيق قانون محيط المعين = 4 × طول الضلع= 4 × 6= 24سم.

• المثال الثاني: معين مساحته 15 وحدة مربعة، وارتفاعه 2، فما هو محيطه؟^[٣]
  • الحل:
  • حساب طول الضلع من قانون مساحة المعين = طول القاعدة × الارتفاع، ومنه 15 = طول القاعدة ×2، وبالتالي فإن طول القاعدة يساوي 7.5سم.
  • تطبيق قانون محيط المعين = 4 × طول الضلع= 4 ×7.5= 30سم.

لمزيد من المعلومات والامثلة حول مساحة المعين يمكنك قراءة المقال الآتي: قانون_حساب_مساحة_المعين.

حساب محيط المعين من طول القطر

• المثال الأول: إذا كان طول قطري المعين (أب ج د)، أج=14سم، ب د=16سم، وكانت (و) نقطة تقاطع قطريه، و(ب ج) قاعدته، جد محيطه.^[٣]
  • الحل:
  • قسمة طول القطرين على 2؛ لحساب طول أو=وج، ب و= ود؛ لأن القطرين ينصّف كل منهم الآخر، ومنه ينتج أن: أو=وج=7سم، ب و= ود=8سم.
  • حساب طول الضلع بتطبيق قانون فيثاغورس على أحد المثلثات القائمة التي يشكلها القطرين مع الأضلاع؛ لأن أقطار المعين متعامدة على بعضها، وبتطبيق قانون فيثاغورس على المثلث (أود) قائم الزاوية في (و) ينتج أن: (أو)²+(ود)²=(أد)²، ومنه (أد)²=(7)²+(8)²= 10.63سم، أي أن طول جمع أضلاع المعين= 10.63سم.
  • حساب محيط المعين بتطبيق قانون: محيط المعين = 4 × طول الضلع= 4 ×10.63=42.52سم.
  • يمكن بدلاً من الخطوات السابقة تعويض القيم في القانون الآتي مباشرة: م=2× ((ق)²+(ل)²)√=م=2× ((16)²+(14)²)√=42.52سم.

• المثال الثاني: إذا كانت مساحة المعين (أب ج د) 64 سم²، وطول قطره (أج) 16سم، جد محيطه.^[٣]
  • الحل:
  • تطبيق قانون مساحة المعين=القطر الأول×القطر الثاني×0.5، ومنه ينتج أن:64=16×القطر الثاني×0.5، وعليه القطر الثاني (ب د)=8سم.
  • قسمة طول القطرين على 2؛ لحساب طول أو=وج، ب و= ود؛ لأن القطرين ينصّف كل منهم الآخر، ومنه ينتج أن أو=وج=8سم، ب و= ود=4سم.
  • حساب طول الضلع بتطبيق قانون فيثاغورس على أحد المثلثات القائمة التي يشكلها القطرين مع الأضلاع؛ لأن أقطار المعين متعامدة على بعضها، وبتطبيق قانون فيثاغورس على المثلث (أود) قائم الزاوية في (و) ينتج أن: (أو)²+(ود)²=(أد)²، ومنه (أد)²=(8)²+(4)²= 8.94سم، أي أن طول جمع أضلاع المعين= 8.94سم.
  • حساب محيط المعين بتطبيق قانون: محيط المعين = 4 × طول الضلع= 4 ×8.94=35.77سم.

• المثال الثالث: إذا كان طول قطر المعين (أب ج د)، أج=16سم، وقياس الزاوية (دأب)= 70 درجة، وكانت (ي) نقطة تقاطع قطريه، و(أب) قاعدته، جد محيطه.^[٢]
  • الحل:
  • وفقاً لخواص المعين فإن القطرين ينصفان زواياه، وينصفان بعضهما البعض، كما أنهما متعامدان على بعضهما، وبالتالي فإن أي=8سم، وقياس الزاوية (ج أب)=35 درجة.
  • حساب طول الضلع (أب) في المثلث (أي ب) قائم الزاوية في (ي) بتطبيق قانون: جتا (ج أ ب)=المجاور÷الوتر=(أب)÷8=جتا(35)=(أب)÷8، ومنه قياس (أب)= 9.768سم؛ أي أن طول جميع أضلاع المعين= 9.768سم.
  • حساب محيط المعين بتطبيق قانون: محيط المعين = 4 × طول الضلع= 4×9.768=39.07سم.

• المثال الرابع: إذا كان طول قطري المعين (أب ج د)، أج=12سم، ب د=5سم، جد محيطه.^[٥]
  • الحل: تعويض القيم في القانون الآتي مباشرة: ح=2× ((ق)²+(ل)²)√، لينتج أن ح=2× ((12)²+(5)²)√=26سم.

المراجع

1. ^ ^{أ ب} “Perimeter Of Rhombus Formula”, byjus.com, Retrieved 14-5-2019. Edited.
2. ^ ^{أ ب ت} “PERIMETER OF RHOMBUS”, www.onlinemath4all.com, Retrieved 18-2-2020. Edited.
3. ^ ^{أ ب ت ث ج} “How to find the perimeter of a rhombus”, www.varsitytutors.com, Retrieved 14-5-2019. Edited.
4. ↑ “Question:”, study.com, Retrieved 18-2-2020. Edited.
5. ↑ “Trapezium, Parallelogram and Rhombus”, www.toppr.com, Retrieved 18-2-2020. Edited.