محتويات
نظرة عامة حول المثلث
يُعرف المُثلث على أنَّه شَكِل مُغلق يحتوي على ثلاثة خطوط مُستقيمة، تلتقي معاً في نقاط معيّنة تُعرف باسم رؤوس المثلث،[١] ويتم تسمية المُثلث نِسبة إلى أسماء رؤوسه، فإذا كانت رؤوس المثلث، هي: الرأس أ، والرأس ب، والرأس ج، فيُعرف المُثلث حينها باسم المثلث (أب ج)، وهكذا.[٢]
لمزيد من المعلومات حول المثلث وخصائصه يمكنك قراءة المقال الآتي: بحث رياضيات عن المثلثات، خصائص المثلث.
أنواع المثلثات
من حيث الزاويا
تصنّف المثلثات حسب قياس زواياها إلى الأنواع الآتية:[١]
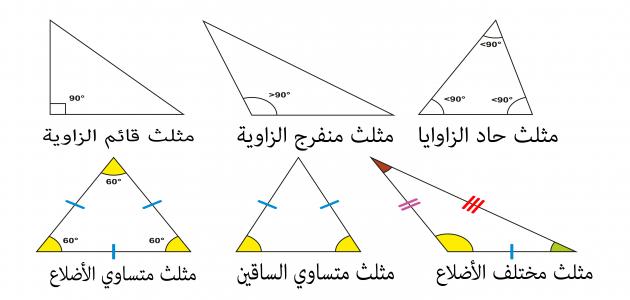
- المُثلثات الحادة: (بالإنجليزية: Acute triangles) يُمكن تَعريف المثلثات الحادة على أنها المُثلثات التي يقل قياس زواياها الثلاث عن 90 درجة؛ فعلى سبيل المثال: المُثلث الحاد أ ب ج، قِياس الزاوية أ ب ج فيه يساوي 78 درجة، وقياس الزاوية ب ج أ يساوي 34 درجة، وقياس الزاوية ج ب أ يساوي 68 درجة.
- المُثلثات مُنفرجة الزاوية: (بالإنجليزية: Obtuse triangles) يُمكن تعريف المُثلثات مُنفرجة الزاوية على أنها مُثلثات يكون فيها قياس زاوية واحدة أكبر من 90 درجة؛ فعلى سبيل المِثال المُثلث أ ب ج، قِياس الزاوية أ ب ج فيه يساوي 40 درجة، وقياس الزاوية ب ج أ يساوي 19 درجة، وقياس الزاوية ج ب أ يساوي 121 درجة.
- المُثلثات قائِمة الزاوية: (بالإنجليزية: Right triangles) يُمكن تعريف المُثلثات قائمة الزاوية على أنها مُثلثات يكون فيها قياس زاوية واحدة يساوي 90 درجة؛ فعلى سبيل المِثال المُثلث أ ب ج، قِياس الزاوية أ ب ج فيه يساوي 90 درجة، وقياس الزاوية ب ج أ يساوي 17 درجة، وقياس الزاوية ج ب أ يساوي 73 درجة.
لمزيد من المعلومات حول زوايا المثلث يمكنك قراءة المقال الآتي: حساب زوايا المثلث.
من حيث الأضلاع
تصنّف المثلثات حسب قياس أضلاعها إلى الأنواع الآتية:[٣]
- مثلث متساوي الأضلاع : (Equilateral Triangle) هو المثلث الذي يتكون من ثلاثة أضلاع متساوية في الطول، وينتج عن هذا التساوي ثلاث زوايا متساوية في القياس، قياس كل منها 60 درجة.
- مثلث متساوي الضلعين، أو متساوي الساقين: (Isosceles Triangle) هو المثلث الذي يتكون من ضلعين متساويين في الطول، وتنتج عن هذا التساوي زاويتان متساويتان في القياس أيضاً، تمثلان الزاويتين المجاورتين للضلعين المتساويين، وهما في الوقت نفسه زاويتا قاعدة المثلث.
- مثلث مختلف الأضلاع: (Scaline Triangle) هو المثلث الذي يحتوي على ثلاثة أضلاع، قياس طول كلٍّ منها مختلف عن الآخر، وبهذا فإن الزوايا أيضاً مختلفة في القياس.
لمزيد من المعلومات حول المثلث متساوي الساقين يمكنك قراءة المقالات الآتية: خصائص المثلث متساوي الساقين، قانون مساحة المثلث متساوي الساقين، قانون محيط المثلث متساوي الساقين.
أمثلة على أنواع المثلثات
- المثال الأول: صنّف المثلثات الآتية حسب معطيات كلٍّ منها:[٤][٥][٦]
- مثلث قياس زواياه الداخلية: (90°,50°,40°).
- مثلث قياس زواياه الداخليّة: (47°,72°,61°).
- مثلث قياس أطوال أضلاعه الثلاث: (6سم، 6سم، 9سم).
- مثلث قياس زواياه الداخلية: (115°,35°,30°).
- مثلث قياس أطوال أضلاعه الثلاث: (9سم، 4سم، 6سم).
- مثلث قياس زواياه: (146°,12°,22°).
- الحل:
| المعطيات | تصنيف المثلث من حيث الأضلاع أو الزوايا |
|---|---|
| مثلث قياس زواياه الداخلية: (47°,72°,61°) | مثلث حاد الزوايا؛ وذلك لأنّ قياس كل زاوية داخلية أقل من 90°، وهو كذلك مختلف الأضلاع. |
| مثلث قياس أطوال أضلاعه الثلاث: (9سم، 4سم، 6سم) | مثلث مختلف الأضلاع؛ وذلك لأنّ طول كلّ ضلع مختلف عن الآخر، وهو أيضاً مثلث مختلف الزوايا. |
| مثلث قياس زواياه الداخلية: (90°,50°,40°) | مثلث قائم الزاوية، وذلك لاحتوائه على زاوية قياسها 90°، وهو كذلك مختلف الأضلاع. |
| **مثلث قياس زواياه الداخلية: (115°,35°,30°) | مثلث منفرج الزاوية؛ وذلك لاحتوائه على زاوية قياسها أكبر من 90°، وهي الزاوية (115)، كما أنه مختلف الأضلاع. |
| مثلث قياس أطوال أضلاعه الثلاث: (6سم، 6سم، 9سم) | مثلث متساوي الساقين. |
| مثلث قياس أطوال أضلاعه الثلاث: (4م، 4م، 4م) | مثلث متساوي الأضلاع، وهو أيضاً متساوي الزوايا. |
| مثلث قياس زواياه: (146°,12°,22°) | مثلث منفرج الزاوية؛ وذلك لاحتوائه على زاوية قياسها أكبر من 90°، وهي الزاوية (146)، كما أنه مختلف الأضلاع. |
لمزيد من المعلومات حول المثلث قائم الزاوية يمكنك قراءة المقالات الآتية: قانون المثلث قائم الزاوية، قانون مساحة المثلث قائم الزاوية، كيفية حساب محيط المثلث القائم.
- المثال الثاني: إذا كانت النسبة بين الزوايا الثلاث لمثلث ما هي: 1:2:3، فما هو نوع هذا المثلث.[٧]
- الحل:
- نفترض أن قياس إحدى الزوايا هو س، وأن قياس الزاويتين المتبقيتين هو: 2س، 3س، ومن خلال معرفة أن مجموع زوايا المثلث= 180درجة، فإن: س+2س+3س=180، ومنه6س=180، وبقسمة الطرفين على 6 ينتج أن: س=30.
- حساب قياس الزاويا:
- الزاوية الأولى=س= 30°.
- الزاوية الثانية=2س=2×30= 60°.
- الزاوية الثالثة=3س=3×30= 90°.
- مما سبق يتبيّن أن هذا المثلث قائم الزاوية؛ لأن قياس إحدى زواياه 90°.
- المثال الثالث: إذا كان قياس إحدى الزوايا المتساوية في المثلث متساوي الساقين هو: 50°، فما هو قياس الزاويتين المتبقيتين.[٨]
- الحل:
- قياس الزاويتين المتساويتين=50°، وبطرح قياس الزاويتين من مجموع زوايا المثلث، يكون قياس الزاوية الثالثة: 180-(50-50)=80°.
- المثال الرابع: إذا كان قياس أضلاع مثلث متساوي الأضلاع: 3س+12، 4س+8، 6س، جد طول كل منها.[٩]
- الحل:
- من خلال تعريف المثلث متساوي الأضلاع ينتج أن: 3س+12=6س، ومنه: س=4، وطول كل ضلع من أضلاع المثلث= 6س= 4×6= 24سم.
لمزيد من المعلومات حول المثلث متساوي الأضلاع يمكنك قراءة المقال الآتي: قانون مساحة المثلث متساوي الأضلاع.
- المثال الخامس: هل المثلث الذي يبلغ طول أضلاعه: 4، 6، 7سم قائم الزاوية.[١٠]
- الحل:
- يمكن معرفة أن هذا المثلث قائم الزاوية من خلال تطبيق نظرية فيثاغورس عليه؛ والتي تنص على أن:
- مربع الضلع الأطول (الوتر)= مجموع مربعي الضلعين الآخرين، ومنه: 7² هل تساوي 6²+4²، بحساب الطرفين ينتج أن: 7²=49، أما 6²+4² فتساوي 52، وعليه هذا المثلث غير قائم الزاوية، وإنما هو مختلف الأضلاع، ولأن مجموع الضلعين أكبر من مربع الوتر، فذلك يدل على أن هذا المثلث حاد الزاوية.
لمزيد من المعلومات حول المثلث قائم الزاوية يمكنك قراءة المقالات الآتية: قانون المثلث قائم الزاوية، قانون مساحة المثلث قائم الزاوية، كيفية حساب محيط المثلث القائم.
- المثال السادس: هل المثلث الذي يبلغ طول أضلاعه: 5، 6،8 سم قائم الزاوية.[١٠]
- الحل:
- يمكن معرفة أن هذا المثلث قائم الزاوية من خلال تطبيق نظرية فيثاغورس عليه؛ والتي تنص على أن:
- مربع الضلع الأطول (الوتر)= مجموع مربعي الضلعين الآخرين، ومنه: 8² هل تساوي 5²+4²، بحساب الطرفين ينتج أن: 8²= 64، أما 6²+5² فتساوي 61، وعليه هذا المثلث غير قائم الزاوية، وإنما هو مختلف الأضلاع، ولأن مجموع الضلعين أقل من مربع الوتر، فذلك يدل على أن هذا المثلث منفرج الزاوية.
لمزيد من المعلومات حول مساحة ومحيط المثلث يمكنك قراءة المقالات الآتية: قانون محيط المثلث، كيف أحسب مساحة المثلث، قانون محيط المثلث ومساحته.
المراجع
- ^ أ ب “The Definition of a Triangle”, www.geom.uiuc.edu, Retrieved 27-4-2019. Edited.
- ↑ “Triangles”, www.mathplanet.com, Retrieved 27-4-2019. Edited.
- ↑ “Triangles”, www.mathsisfun.com, Retrieved 20-12-2017. Edited.
- ↑ “Triangles”, www.mathopolis.com, Retrieved 7-4-2020. Edited.
- ↑ “Types of Triangles”, www.mathwarehouse.com, Retrieved 7-4-2020. Edited.
- ↑ “Triangles Classification”, www.math10.com, Retrieved 7-4-2020. Edited.
- ↑ Geoff Pilling, Eli Ross, and Jimin Khim , “Classification of Triangles”، brilliant.org, Retrieved 7-4-2020. Edited.
- ↑ “classification of triangles”, www.aplustopper.com, Retrieved 7-4-2020. Edited.
- ↑ “Triangle Classifications”, www.wyzant.com, Retrieved 7-4-2020. Edited.
- ^ أ ب “The Converse of the Pythagorean Theorem”, www.murrieta.k12.ca.us, Retrieved 7-4-2020. Edited.