قانون حفظ المادة

• ذات صلة
• ما هو قانون حفظ الكتلة
• ما هو قانون حفظ الطاقة

تعريف قانون حفظ المادة

ينصّ القانون العام لحفظ المادة أو حفظ الكتلة (بالإنجليزية: Law of Conservation of Mass) على أنّ المادة في النظام المغلق لا يمكن أن تفنى ولا تُستحدث، ولكن تبقى محفوظة وتتحول من شكل إلى آخر، والمقصود بالنظام المغلق هو النظام الذي لا تتفاعل به المادة مع ما يُحيط بها.^[١]

ومن الجدير بالذكر أنّه وبعد التوصل إلى قانون حفظ المادة عُدّل عليه وطُوّر من قِبل العلماء في مجال الكيمياء ومجال الميكانيكا،^[٢] وأصبح القانون قابلًا للتطبيق في مجال الكيمياء والفيزياء.^[٣]

قانون حفظ المادة في الكيمياء

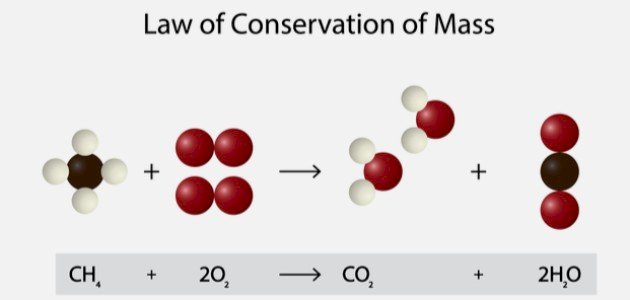
ينص قانون حفظ المادة في الكيمياء على أنّه في التفاعلات الكيميائية تكون كتلة المواد الناتجة من التفاعل مساويةً لكتلة المواد المتفاعلة، بحيث يجري التفاعل في نظام مغلق، وبغض النظر عن أيّة تحولات في المادة أو التفاعلات الكيميائية التي من الممكن أن تتعرض لها المواد، إلا أنّ المهم هو بقاء كتلة المواد كما هي.^[١]

يُعدّ قانون حفظ المادة مهمًا جدًا للعلماء في مجال الكيمياء، إذ ساعد العلماء على فهم حقيقة أنّ المواد لا تختفي كنتيجة لحدوث تفاعل معين، لكن ما يحصل هو تحول المواد من شكل إلى آخر مع الاحتفاظ بنفس الكتلة.^[١]

ساهم عدد من العلماء في تطوير قانون حفظ المادة، ومن أشهرهم العالم الفرنسي أنطوان لافوازييه الذي قدّم إثباتات لبرهنة هذا القانون، وقد سمّى البعض قانون حفظ المادة بقانون لافوازييه (بالإنجليزية: Lavoisier’s Law) تكريمًا لإنجازاته وجهوده في هذا المجال.^[١]

صيغة القانون وأمثلة عليه

تكون صيغة قانون حفظ المادة في مجال الكيمياء كالآتي:^[٣]

كتلة المواد المتفاعلة = كتلة المواد الناتجة

أمثلة على قانون حفظ المادة

فيما يأتي بعض الأمثلة على قانون حفظ المادة في الكيمياء:

• عند تسخين 10 غ من كربونات الكالسيوم (CaCO3)، ينتج من التفاعل 4.4 غرام من ثاني أكسيد الكربون (CO2) إضافةً إلى 5.6 غ من أكسيد الكالسيوم (CaO)، أثبت أنّ هذا التفاعل خاضع لقانون حفظ المادة.

الحل:

• كتلة المواد المتفاعلة = كتلة المواد الناتجة
• 10 غ من (CaCO3) = 4.4 غ من (CO2) + 5.6 غ من (CaO)
• 10 غ من المواد المتفاعلة = 10 غ من المواد الناتجة، ممّا يعني أنّ هذا التفاعل يخضع لقانون حفظ المادة.

• يتفاعل هيدروكسيد البوتاسيوم (KOH) مع ثاني أكسيد الكربون (CO2) لإنتاج كربونات البوتاسيوم (K2CO3) والماء (H2O)، كم غرام ينتج من كربونات البوتاسيوم إذا تفاعل 224.4 غ من (KOH)، مع 88.0 غ من (CO2)، وأنتج التفاعل ماء بوزن 36.0 غ؟

الحل:

• حساب كتلة المواد المتفاعلة.
• كتلة المواد المتفاعلة = 224.4 غ (KOH) + 88.0 غ (CO2) = 312.4 غ من ثاني أكسيد الكربون وكربونات البوتاسيوم.
• كتلة المواد المتفاعلة = كتلة المواد الناتجة
• لحساب وزن كربونات البوتاسيوم لوحدها: 312.4 غ – 36 غ وزن الماء =276.4 غ وزن كربونات البوتاسيوم الناتجة.

تطبيقات عملية في مجال الكيمياء

يُمكن تطبيق قانون حفظ المادة على العديد من أوجه الحياة المختلفة، وفيما يأتي بعض من الأمثلة اليومية في الحياة على قانون حفظ المادة:

إشعال النيران

عند جمع أعواد من الخشب وإشعال النيران فيها، قد يعتقد البعض أن أعواد الخشب احترقت واختفت، لكن في الحقيقة، أثناء احتراق الأعواد الخشبية فإنّها تتفاعل مع الأكسجين الموجود في الهواء المحيط، لتتحول وتعطي الرماد وغاز ثاني أكسيد الكربون، إضافةً إلى بخار الماء الناتج.^[٤]

كنتيجة لذلك عند جمع الكتلة للأعواد الخشبية والأكسجين الداخل في التفاعل الكيميائي قبل إضرام النار بهم، ستتساوى الكتلة النهائية مع كتلة الرماد المُحترق، وغاز ثاني أكسيد الكربون، وبخار الماء المُتصاعد.^[٤]

الشمعة المحترقة

تتكوّن الشمعة من الشمع والفتيلة الموجودة فيها، وعند إحراق الشمعة كاملةً يمكن ملاحظة أنّ الكمية المتبقية من الشمع أقلّ بكثير ممّا كانت عليه قبل إحراقها، وهذا يعني أنّ الشمع المحروق والذي كان قد اختفى قد تحول إلى غازات مختلفة مثل ثاني أكسيد الكربون، وبخار الماء، ممّا يُشير إلى أنّ كتلة المواد المتفاعلة يساوي كتلة المواد الناتجة باختلاف حالتها عند حساب ذلك ولا توجد كتلة ضائعة بينهما.^[٤]

ينص قانون حفظ المادة في الكيمياء على أنّ كتلة المواد المتفاعلة تساوي كتلة المواد الناتجة من التفاعل، ويُعدّ أنطوان لافوازييه من أهمّ العلماء الذين ساهموا في إيجاد هذا القانون، ومن التطبيقات العملية على قانون حفظ المادة في الكيمياء؛ إشعال النيران.

قانون حفظ المادة في الميكانيكا

يُعبّر عن قانون حفظ المادة في مجال الميكانيكا عن طريق استخدام معادلة الاستمرارية (بالإنجليزية: continuity equation) في ميكانيكا الموائع وميكانيكا الاستمرارية،^[٥] إذ تنص معادلة الاستمرارية على أنّه في الحالة المستقرة يكون معدل تدفق الكتلة إلى النظام مساويًا لمعدل تدفق الكتلة خارج النظام.^[٦]

تصف المعادلة حركة بعض المواد كالغازات والسوائل، وكيفية احتفاظها بكتلتها أثناء الحركة.^[٦]

صيغة القانون وأمثلة عليه

يُستخدم القانون الآتي للتعبير عن قانون حفظ المادة فيزيائيًا:^[٧]

الكتلة المتغيرة في النظام= (الكثافة × السرعة × المساحة × الزمن) الداخلة في النظام – (الكثافة × السرعة × المساحة × الزمن) الخارجة من النظام

وبالرموز:

dM = ρi vi Ai dt – ρo vo Ao dt

حيث إنّ:

• dM: تغيّر الكتلة في النظام (كغ).
• ρ: الكثافة (كغ/ م³)
• v: السرعة (م/ ث).
• A: المساحة (م2).
• dt: الزيادة في الزمن (ث).
• i: الداخلة في النظام.
• o: الخارجة من النظام.

أمثلة على قانون حفظ المادة

فيما يأتي بعض الأمثلة على قانون حفظ المادة في مجال الميكانيكا:

• يتمّ تعبئة خزان بماء له كثافة تساوي 1000 كغ/ م³، بسرعة 2 م/ ث، من خلال أنبوب نصف قطره يساوي 25 ملم، وفي نفس الوقت يخرج الماء من الخزان من خلال أنبوب آخر نصف قطره 15 ملم، بسرعة 2.5 م/ ث، احسب التغيّر في محتوى الخزان من الماء بعد مدة 20 دقيقة.

الحل:

• من أجل التعويض في قانون حفظ المادة يلزم ما يأتي:
• إيجاد مساحة الأنبوب من خلال قانون مساحة الدائرة:
• المساحة = π × نق²
• المساحة الثانية = π × (0.025)²
• 0.0019625 ملم2
• المساحة الأولى = π × (0.015)²
• 0.0007065 ملم²
• تحويل الزمن من دقائق إلى ثواني: 20 دقيقة × 60 ثانية/ دقيقة = 1200 ثانية
• الكتلة المتغيرة في النظام= (الكثافة × السرعة × المساحة × الزمن) الداخلة في النظام – (الكثافة × السرعة × المساحة × الزمن) الخارجة من النظام
• التغيّر في محتوى الخزان من الماء بعد 20 دقيقة = (1000 × 2 × 0.0019625 × 1200) – (1000 × 2.5 × 0.0007065 × 1200) = 2590.5 كغ

• سائل ذو كثافة 5000 كغ/ م³، يتم تعبئته في وعاء بسرعة 5 م/ ث، من خلال أنبوب بقطر 100 ملم، وفي نفس الوقت يسيل السائل من الوعاء بسرعة 1 م/ث، بأنبوب قطره 200 ملم، احسب محتوى الوعاء من السائل المتبقي بعد 15 دقيقة.

الحل:

• من أجل التعويض في قانون حفظ المادة يلزم ما يأتي:
• إيجاد مساحة الأنبوب من خلال قانون مساحة الدائرة:
• المساحة = π × نق² أو π × (القطر/2)²
  • المساحة الثانية = π × (0.1/2)²
  • 0.00785
  • المساحة الأولى = π × (0.2/2)²
  • 0.0314
• تحويل الزمن من دقائق إلى ثواني: 15 دقيقة × 60 ثانية/ دقيقة = 900 ثانية
• الكتلة المتغيرة في النظام= (الكثافة × السرعة × المساحة × الزمن) الداخلة في النظام – (الكثافة × السرعة × المساحة × الزمن) الخارجة من النظام
• التغيّر في محتوى الخزان من الماء بعد 15 دقيقة = (5000 × 5 × 0.00785 × 900) – (5000 × 1 × 0.0314 × 900) = 35325 كغ

تطبيقات عملية في مجال الميكانيكا

يُمكن تطبيق قانون حفظ المادة في مجال الميكانيكا في أوجه الحياة المختلفة، وفيما يأتي بعض الأمثلة:^[٨]

• عملية جريان المياه في الأنابيب أو في الخرطوم تُفسّر وِفقًا لقانون حفظ المادة ومعادلة الاستمرارية، حيث تحتفظ بكتلتها أثناء الحركة.
• جريان الأنهار، وجريان الغازات في الأنابيب، حيث تحتفظ بكتلتها أثناء الحركة.

يُعرّف قانون حفظ المادة على أنّ المواد لا يُمكن أن تُفنى ولا أن تُستحدث، إنّما تتحول من شكل إلى آخر، حيث ساعد القانون العلماء على تفسير العديد من الظواهر المختلفة، كظاهرة اختفاء المواد كنتيجة للتفاعل، إذ إنّ المواد المتفاعلة لم تختفِ، إنّما تحولت لشكل آخر، ويُطبّق هذا القانون أيضًا في مجال الميكانيكا، واستخدم لتفسير العديد من الظواهر، مثل جريان الأنهار.

المراجع

1. ^ ^{أ ب ت ث} “definition-of-conservation-of-mass-law”, thoughtco, Retrieved 14/9/2021. Edited.
2. ↑ “Law Of Conservation Of Mass”, byjus, Retrieved 14/9/2021. Edited.
3. ^ ^{أ ب} “3.7: Conservation of Mass – There is No New Matter”, chem, Retrieved 14/9/2021. Edited.
4. ^ ^{أ ب ت} “2 Easy Examples of the Law of Conservation of Mass”, prepscholar, Retrieved 14/9/2021. Edited.
5. ↑ “Law of Conservation of Mass”, byjus, Retrieved 14/9/2021. Edited.
6. ^ ^{أ ب} “Continuity Equation”, byjus, Retrieved 14/9/2021. Edited.
7. ↑ “Conservation of Mass”, engineeringtoolbox, Retrieved 22/9/2021. Edited.
8. ↑ “continuity-equation”, byjus, Retrieved 14/9/2021. Edited.