محتويات
حساب مساحة المُعين
تمثل مساحة المُعين (بالإنجليزية: Rhombus Area)-كمساحة غيره من الأشكال الهندسية- المنطقة الداخلية الموجودة ضمن حدوده،[١] ويمكن حساب مساحة المُعين بأكثر من طريقة، ومن هذه الطرق:[٢][٣]
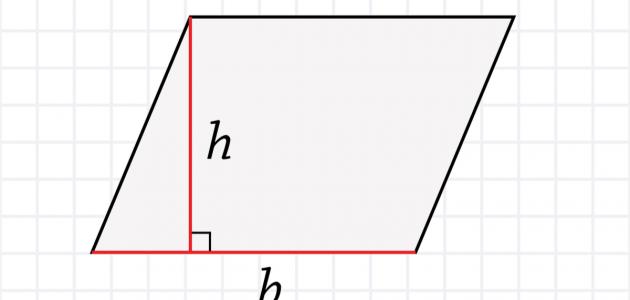
- حساب المساحة بدلالة الارتفاع وطول أحد الأضلاع: يمكن حساب مساحة المعين بدلالة ارتفاعه وطول أحد أضلاعه باستخدام القانون الآتي:
- مساحة المعين= الارتفاع × طول الضلع، وبالرموز: م=ع×ل؛ حيث إن ارتفاع المُعين (ع) هو عبارة عن القطعة المستقيمة العمودية الواصلة بين الضلعين المقابلين لبعضهما، أما بالنسبة لطول الضلع فيمكن اختيار طول أي ضلع؛ لأن جميع أضلاع المُعين متساوية في الطول.
- حساب المساحة بدلالة طولي القطرين: يمكن حساب مساحة المُعين بدلالة طولي قطريه؛ حيث يمكن تعريف قطري المُعين بأنهما القطعتان المستقيمتان الواصلتان بين كل زوج من الزوايا المتقابلة، وذلك باستخدام القانون الآتي:
- مساحة المعين= ((القطر الأول×القطر الثاني)÷2)، وبالرموز: م= (ق×ل)/2.
- حساب المساحة بدلالة طول ضلع وقياس إحدى زواياه: يمكن من خلال هذه الطريقة حساب مساحة المُعين في حال كان طول الضلع وقياس إحدى زواياه معلومين، والقانون هو:
- مساحة المُعين= مربع طول ضلع المعين×جيب إحدى زوايا المعين، ويعبر عنه بالرموز كالآتي: م= (ل)²×جا(α).
لمزيد من المعلومات والأمثلة حول ارتفاع المعين يمكنك قراءة المقال الآتي: ارتفاع المعين.
لمزيد من المعلومات والأمثلة حول محيط المعين يمكنك قراءة المقال الآتي: قانون محيط المعين.
أمثلة متنوعة على حساب مساحة المعين
حساب المساحة بدلالة طول ضلع وقياس إحدى زواياه
- المثال الأول: احسب مساحة لوح خشبي على شكل مُعين إذا علمت طول أحد أضلاعه يساوي 2م، وقياس إحدى زواياه يساوي 60درجة.[٢]
- الحل: بتطبيق قانون مساحة المُعين بدلالة طول ضلع وقياس إحدى زواياه= (ل)²×جا الزاوية، وتعويض قيمة طول الضلع وقياس الزاوية بالقانون.
- مساحة اللوح الخشبي = (2م)² ×جا(60°)=4م²×جا60°=4م²×0.866، إذن مساحة اللوح الخشبي = 3.46م².
- المثال الثاني: احسب مساحة المُعين إذا علمت طول أحد أضلاعه يساوي10م، وقياس زواياه يساوي 60درجة، 120 درجة.[٤]
- الحل: بتطبيق قانون مساحة المُعين بدلالة طول ضلع وقياس إحدى زواياه= (ل)²×جا الزاوية، نعوض قيمة طول الضلع وقياس الزاوية بالقانون، لينتج أن م= (10م)² ×جا(120°)=100م²×0.866، إذن مساحة المعين= 86.6م².
حساب المساحة بدلالة طولي القطرين
- المثال الأول: احسب مساحة مُعين إذا علمت أن طول قطريه يساوي 6 سم، و8 سم.[٣]
- الحل: بتطبيق قانون مساحة المُعين بدلالة قطريه= (ق× ل×0.5).
- نعوّض قيمة القطرالأول والقطر الثاني بالقانون، لينتج أن مساحة المُعين = (0.5× 8× 6)= 24سم².
- المثال الثاني: احسب مساحة مُعين إذا علمت أن طول قطريه يساوي 10 سم، و8 سم.[٥]
- الحل: بتطبيق قانون مساحة المُعين بدلالة قطريه= (ق× ل×0.5).
- نعوّض قيمة القطرالأول والقطر الثاني بالقانون، لينتج أن مساحة المُعين = (0.5× 8× 10)= 40سم².
- المثال الثالث: إذا كانت مساحة مُعين 240سم²، جد طول قطره الآخر إذا كان طول أحد قطريه يساوي 16 سم.[٥]
- الحل: تطبيق قانون مساحة المُعين بدلالة قطريه: م=(ق× ل×0.5).
- تعويض قيمة القطرالأول والمساحة بالقانون، لينتج أن 240= (0.5× ل× 16)، ومنه ل=30سم.
- المثال الرابع: إذا كانت هناك غرفة مكونة من 3000 بلاطة على شكل معين، طول قطري كل منها 45سم، 30سم، جد تكلفة تلميع أرضية الغرفة إذا كانت تكلفة التلميع تساوي 4 دولارات لكل متر مربع.[٥]
- الحل:
- تطبيق قانون مساحة المُعين بدلالة قطريه= (ق× ل×0.5)، لينتج أن مساحة المُعين = (0.5× 45× 30)= 675سم²؛ أي أن مساحة البلاطة الواحدة 675 سم².
- حساب المساحة الكلية لأرضية الغرفة=مساحة البلاطة الواحدة×عدد البلاطات= 675سم²×3000=2,025,000سم².
- تحويل المساحة من سم² إلى م²، لينتج أن مساحة الغرفة= 202.5م².
- حساب تكلفة تلميع البلاط= تكلفة تلميع المتر المربع الواحد×مساحة الغرفة=(4 دولار/م²) × 202.5م²=810 دولارات.
- المثال الخامس: يبلغ طول الضلع أد في المعين أب ج د 13سم، وطول القطر (ب د) 10سم، فإذا كان الضلع ب ج هو القاعدة، والنقطة (و) نفطة تقاطع القطرين (ب د)، (أج)، جد مساحة هذا المعين.[٦]
- الحل: تطبيق نظرية فيثاغورس على المثلث أود قائم الزاوية في و؛ لإيجاد طول القطر الثاني (أج)؛ حيث إن قطري المعين متعامدان على بعضهما وينصف كل منهم الآخر حسب خواص المعين؛ لينتج أن (أد)²=(أو)²+(ود)²=(13)²=(أو)²+(5)²، ومنه (أو)=12سم، وعليه (أج)=2×12=24سم.
- تطبيق قانون مساحة المُعين بدلالة قطريه: م=(ق× ل×0.5).
- تعويض قيمة القطرالأول والثاني بالقانون، لينتج أن م= (0.5× 24× 10)، ومنه م=120سم².
- المثال السادس: إذا كان طول القطر الأول للمعين أب ج د= (ق)=10سم، وطول قطره الآخر ل= 0.5ق، جد مساحته.[٦]
- الحل: تطبيق قانون مساحة المُعين بدلالة قطريه: م=(ق× ل×0.5).
- تعويض قيمة القطرالأول والمساحة بالقانون، لينتج أن م= ((0.5×10)×10×0.5)=25سم².
- المثال السابع:إذا كان طول أحد أقطار المعين= ق سم، وطول القطر الآخر= 3+ق سم، وكانت مساحة المعين = 14سم²، جد طول قطريه.[٧]
- الحل: تطبيق قانون مساحة المُعين بدلالة قطريه: م=(ق× ل×0.5)
- تعويض قيمة القطرالأول والثاني والمساحة بالقانون، لينتج أن: 14=ق×(3+ق)×0.5، ومنه 28=3ق+ق²، وبحل المعادلة التربيعية 0=28-3ق+ق²، ينتج أن ق=7،4- سم، وباستبعاد القيمة السالبة ينتج أن ق=4سم؛ أي أن طول القطر الأول (ق) = 4سم، وطول القطر الثاني (ل)=4+3=7سم.
حساب المساحة بدلالة الارتفاع وطول أحد الأضلاع
- المثال الأول: احسب مساحة مُعين إذا علمت أن ارتفاعه يساوي 6 سم، وطول أحد أضلاعه 2 سم.[٢]
- الحل: بتطبيق قانون مساحة المُعين بدلالة الارتفاع وطول ضلعه: المساحة= الارتفاع ×طول الضلع، وتعويض قيمة الارتفاع وطول الضلع بالقانون، لينتج أن مساحة المُعين = 6سم ×2سم، إذن مساحة المُعين =12سم².
- المثال الثاني: احسب مساحة مُعين إذا علمت أن ارتفاعه يساوي 4 سم، وطول أحد أضلاعه 6سم، ثم جد طول قطره الآخر إذا كان طول قطره الأول=8سم.[٥]
- تطبيق قانون مساحة المُعين بدلالة الارتفاع وطول ضلعه: المساحة= الارتفاع ×طول الضلع، وتعويض قيمة الارتفاع وطول الضلع بالقانون، لينتج أن مساحة المُعين = 6سم ×4سم، إذن مساحة المُعين =24سم².
- تطبيق قانون مساحة المعين بدلالة طول القطرين، لإيجاد طول القطر الثاني: م=(ق× ل×0.5)، 24=(8× ل×0.5)، ومنه ل=6سم.
- المثال الثالث: إذا كانت مساحة مُعين 64سم²، جد ارتفاعه إذا علمت ان طول أحد أضلاعه 8سم.[٨]
- الحل:
- تطبيق قانون مساحة المُعين بدلالة الارتفاع وطول ضلعه: المساحة= الارتفاع ×طول الضلع، تعويض المساحة وطول الضلع بالقانون، لينتج أن 64= الارتفاع×8، ومنه الارتفاع=8سم.
- المثال الرابع: إذا كانت مساحة مُعين 315سم²، ومحيطه 180سم، جد ارتفاعه.[٩]
- الحل:
- إيجاد طول الضلع عن طريق قسمة محيط المعين على أربعة، لينتج أن طول الضلع=180/4=45سم.
- تطبيق قانون مساحة المُعين بدلالة الارتفاع وطول ضلعه: المساحة= الارتفاع ×طول الضلع، تعويض المساحة وطول الضلع بالقانون، لينتج أن 315= الارتفاع×45، ومنه الارتفاع=7سم.
فيديو عن المعين وحساب مساحته
تعرف على المعين و كيفية حساب مساحته في الفيديو:[١٠]
المراجع
- ↑ “Rhombus. Formulas, characterizations and properties of rhombus”, onlinemschool.com, Retrieved 17-2-2020. Edited.
- ^ أ ب ت “Measuring the Area of a Rhombus: Formula & Examples”, www.study.com, Retrieved 2-12-2017. Edited.
- ^ أ ب “Rhombus”, www.mathsisfun.com, Retrieved 1-12-2017. Edited.
- ↑ “How To Find the Area of a Rhombus”, tutors.com, Retrieved 17-2-2020. Edited.
- ^ أ ب ت ث “Area of Rhombus”, www.teachoo.com, Retrieved 17-2-2020. Edited.
- ^ أ ب “Example Questions”, www.varsitytutors.com, Retrieved 17-2-2020. Edited.
- ↑ “area of a rhombus formula”, www.vedantu.com, Retrieved 18-2-2020. Edited.
- ↑ “How to Find the Height of a Rhombus”, sciencing.com, Retrieved 17-2-2020. Edited.
- ↑ “Area of Rhombus”, www.math-only-math.com, Retrieved 17-2-2020. Edited.
- ↑ فيديو عن المعين وحساب مساحته.