مساحة الشبه المنحرف

'); }

مساحة شبه المنحرف

يمكن حساب مساحة شبه المنحرف باستخدام أحد القوانين أو الطرق الآتية:^[١]

• عند معرفة طول القاعدتين والارتفاع:
  • مساحة شبه المنحرف = ½ × (طول القاعدة الأولى+طول القاعدة الثانية)×الارتفاع، وبالرموز:
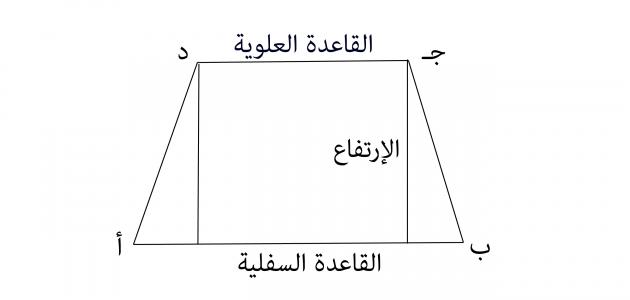
  • م= ½×(أ+ب)×ع؛ حيث:
    • م: مساحة شبه المنحرف.
    • أ: طول القاعدة السفلية.
    • ب: طول القاعدة العلوية.
    • ع: الارتفاع.
• استخدام صيغة هيرون: وذلك عند معرفة أطوال جميع الأضلاع دون معرفة الارتفاع، والتي تنص على أن:
  • م=((و-أ)(و-ب)(و-أ-ج)(و-أ-د))√×(أ+ب)/(|أ-ب|)؛ حيث:
    • م: مساحة شبه المنحرف.
    • أ: طول القاعدة السفلية.
    • ب: طول القاعدة العلوية.
    • ج،د: طول الساقين.
    • و: نصف محيط شبه المنحرف، وهو يساوي: و=(أ+ب+ج+د)÷2.
• عند معرفة طول الخط المستقيم المتوسط:^[٢]
  • مساحة شبه المنحرف = طول الخط المتوسط×الارتفاع، وبالرموز:
  • م=ط×ع؛ حيث:
  • طول الخط المتوسط (ط)=2/(أ+ب).
• عند معرفة إحدى القاعدتين: يُمكن حساب مساحة شبه المنحرف عند معرفة طول إحدى القاعدتين، والارتفاع، وطول ضلع من الأضلاع غير المتوازية، وذلك كالآتي:^[٣]
  • تقسيم شبه المنحرف إلى مثلثين بإسقاط عمودين من زوايا القاعدة الأولى إلى القاعدة الثانية.
  • تطبيق نظرية فيثاغورس لكل مثلث على حدة، لإيجاد طول قاعدة المثلث المجهولة كالآتي:(الوتر)² = (الضلع الأول)² + (الضلع الثاني)².
  • حساب طول القاعدة الثانية المجهولة لشبه المنحرف بجمع طول القاعدة الأولى معروفة القيمة إلى مجموع قاعدتي المثلثين.
  • تطبيق معادلة مساحة شبه المنحرف: مساحة شبه المنحرف = ½ × (طول القاعدة الأولى + طول القاعدة الثانية) × الارتفاع.

لمزيد من المعلومات والامثلة حول مساحة شبه المنحرف القائم يمكنك قراءة المقال الآتي: مساحة شبه المنحرف القائم.
لمزيد من المعلومات والامثلة حول شبه المنحرف يمكنك قراءة المقال الآتي: بحث عن شبه المنحرف.
لمزيد من المعلومات والامثلة حول خصائص شبه المنحرف يمكنك قراءة المقال الآتي: خصائص الشبه منحرف.

'); }

أمثلة متنوعة على حساب مساحة شبه المنحرف

• المثال الأول: شبه منحرف، فيه طول القاعدة الأولى=4سم، وطول القاعدة الثانية= 6سم، أما ارتفاعه= 3سم، جد مساحته.^[٤]
  • الحل:
    • بتطبيق قانون مساحة شبه المنحرف= 0.5×(طول القاعدة الأولى+طول القاعدة الثانية)× الارتفاع.
    • مساحة شبه المنحرف=3×(4+6)× 0.5
    • مساحة شبه المنحرف= 3×(10)× 0.5
    • مساحة شبه المنحرف= 3×5
    • إذن: مساحة شبه المنحرف= 15سم².

• المثال الثاني: شبه منحرف، فيه مجموع طولي القاعدتين يساوي62 دسم، أما ارتفاعه فيساوي 18 دسم، احسب مساحة شبه المنحرف.^[٥]
  • الحل: بتطبيق قانون مساحة شبه المنحرف= 0.5×(طول القاعدة الأولى+طول القاعدة الثانية)× الارتفاع، ومنه مساحة شبه المنحرف=0.5×(62)× 18=558 دسم².

• المثال الثالث: شبه منحرف فيه طول القاعدة العلوية=21سم، وطول القاعدة السفلية= 31سم، وارتفاعه= 5سم، جد مساحته.^[٦]
  • الحل:
    • بتطبيق قانون مساحة شبه المنحرف= 0.5×(طول القاعدة الأولى+طول القاعدة الثانية)× الارتفاع.
    • م=0.5×(21+31)×5=130سم².

لمزيد من المعلومات والامثلة حول ارتفاع شبه المنحرف يمكنك قراءة المقال الآتي: ارتفاع شبه المنحرف.

• المثال الرابع: شبه منحرف فيه طول القاعدة العلوية=15سم، وطول القاعدة السفلية= 11سم، ومساحته=52سم²، جد ارتفاعه.^[٧]
  • الحل:
    • بتطبيق قانون مساحة شبه المنحرف= 0.5×(طول القاعدة الأولى+طول القاعدة الثانية)× الارتفاع.
    • 52=0.5×(15+11)×ع، ومنه ع=4سم.

• المثال الخامس: رف مكتبة على شكل شبه منحرف متساوي الساقين، طول قاعدته السفلية=2م، وطول قاعدته العلوية 8م، وسمكه 8سم، جد مساحة هذا الرف.^[٨]
  • الحل:
    • يجب أولاً توحيد الوحدات لتكون جميعها بالمتر، وعليه سمك الرف=8سم=0.08م.
    • تطبيق قانون مساحة شبه المنحرف= 0.5×(طول القاعدة الأولى+طول القاعدة الثانية)× الارتفاع.
    • م=0.5×(8+2)×0.08، ومنه م=0.4م؛ أي أن مساحة رف المكتبة= 0.4م.

• المثال السادس: المستطيل (ي ج ت ر)، فيه النقطة (م) تقع في منتصف القاعدة (ج ت)، وطول الضلع (ي ر) فيه=2س، والضلع (رت)=0.5س، إذا تم وصل خط بين النقطتين (ي م)، ليتكون شبه المنحرف (ي م ت ر) قاعدته الصغرى (م ت)، ومساحته 1200وحدة مربعة، جد قيمة س.^[٨]
  • الحل:
    • حساب طول (م ت)، وهو يساوي س؛ لأن النقطة م تنصّف قاعدة المستطيل (س ت) التي يبلغ طولها 2س.
    • تطبيق قانون مساحة شبه المنحرف= 0.5×(طول القاعدة الأولى+طول القاعدة الثانية)× الارتفاع، م=1200=0.5×(2س+س)× 0.5س، ومنه 3/4 س²=1200، ومنه: س= 40 وحدة طول.

• المثال السابع: شبه المنحرف (أب ج د) قائم الزاوية في (د) فيه طول القاعدة العلوية (أب)=20سم، والقاعدة السفلية (ج د)=25سم، والضلع (أ ج)= 13سم، جد مساحته.^[٩]
  • الحل:
    • يجب أولاً حساب الارتفاع والذي يمكن حسابه عن طريق إسقاط عمود من الزاوية (أ) إلى القاعدة (ج د) ولنفرض أنه (أو) وهو يساوي الارتفاع.
    • حساب طول (وج)، وهو يساوي طول القاعدة السفلية (ج د)-طول القاعدة العلوية (أب): (وج)=25-20=5سم
    • تطبيق نظرية فيثاغورس على المثلث (أوج) قائم الزاوية في (و)، لينتج أن: (أو)²+(وج)²=(أج)²، ومنه (13)²=(5)²+(أو)²، ومنه (أو)=12سم؛ أي أن الارتفاع=12سم.
    • تطبيق قانون مساحة شبه المنحرف= 0.5×(طول القاعدة الأولى+طول القاعدة الثانية)× الارتفاع، م=0.5×(20+25)×12=270سم².

• المثال الثامن: شبه المنحرف (أب ج د) فيه طول القاعدة العلوية (د ج)=12سم، والقاعدة السفلية (أب)=36سم، والضلع (ب د)=(أج)= 15سم، جد مساحته.^[٩]
  • الحل:
    • شبه المنحرف هذا فيه كل الأضلاع معلومة دون معرفة الارتفاع؛ لذلك لإيجاد مساحته يمكن استخدام صيغة هيرون: م=((و-أ)(و-ب)(و-أ-ج)(و-أ-د))√×(أ+ب)/(|أ-ب|)، ولاستخدامها يجب أولاً حساب و=2/محيط شبه المنحرف= 2/(12+36+15+15)=39سم.
    • تعويض الأرقام في الصيغة السابقة: م=((و-أ)(و-ب)(و-أ-ج)(و-أ-د))√×(|أ-ب|)/(أ+ب)=((39-36)(39-12)(39-36-15)(39-36-15))√×(36+12)/(|36-12|)=((3)(27)(12-)(12-)√2=108×2=216سم².

• المثال التاسع: إذا كانت مساحة شبه المنحرف= 165سم²، وفيه طول القاعدة السفلي يساوي ضعف طول القاعدة العلوية، وارتفاعه=10سم، جد طول القاعدتين.^[٩]
  • الحل:
    • نفترض أن طول القاعدة العلوية=س، وطول القاعدة العلوية = 2س، وبتطبيق قانون مساحة شبه المنحرف= 0.5×(طول القاعدة الأولى+طول القاعدة الثانية)× الارتفاع، ينتج أن 165=0.5×(2س+س)×10، ومنه س=11سم، أي طول القاعدة العلوية=11سم، وطول القاعدة السفلية=2س=22سم.

• المثال العاشر: إذا كان هناك مربع (أب ج د) طول ضلعه=4سم، تشكّل النقطة (و) نقطة المنتصف في القاعدة (ب ج)، جد مساحة شبه المنحرف المتشكّل عند وصل النقطة (و) بالنقطة (د).^[١٠]
  • الحل:
    • شبه المنحرف المتشكّل هو (ب و دأ)، فيه طول (ب و) أو القاعدة العلوية=2سم لأن النقطة (و) تقع في منتصف الضلع (ب ج)، وطول القاعدة السفلية (أد)=4سم من المعطيات، أما ارتفاعه (أب) فهو أيضاً=4سم من المعطيات.
    • تطبيق قانون مساحة شبه المنحرف= 0.5×(طول القاعدة الأولى+طول القاعدة الثانية)× الارتفاع، ومنه م=0.5×(4+2)×4=12سم².

• المثال الحادي عشر: إذا كانت مساحة حقل على شكل شبه منحرف= 480م²، وكانت المسافة الواصلة بين ضلعيه المتوازيين=15م، وطول قاعدته السفلية= 20م، جد طول قاعدته العلوية.^[١١]
  • الحل: بتطبيق قانون مساحة شبه المنحرف= 0.5×(طول القاعدة الأولى+طول القاعدة الثانية)× الارتفاع، ومنه 480=0.5×(20+طول القاعدة العلوية)×15، ومنه طول القاعدة العلوية=44م.

• المثال الثاني عشر: يريد أحمد شراء قطعة أرض مساحتها 10,500م² على شكل شبه منحرف، إذا كان طول حافتها على طول الطريق العام تساوي نصف طول حافتها على طول النهر، وطول المسافة العمودية الواصلة بين الحافتين تساوي 100م، جد طول حافة قطعة الأرض على النهر.^[١١]
  • الحل: نفترض أن طول حافتها على النهر يساوي س، وطول حافتها على الطريق العام= 0.5س، ثم بتطبيق قانون مساحة شبه المنحرف= 0.5×(طول القاعدة الأولى+طول القاعدة الثانية)× الارتفاع، ومنه 10500=0.5×(س+0.5س)× 100، ومنه س=140م؛ أي أن طول حافتها على طول النهر=140م، زطول حافتها على الطريق العام= 0.5س=70م.

لمزيد من المعلومات والامثلة حول قوانين شبه المنحرف يمكنك قراءة المقال الآتي: قوانين شبه المنحرف.

• المثال الثالث عشر: شبه المنحرف (أب ج د) فيه طول القاعدة السفلية (د ج)=25سم، والقاعدة العلوية (أب)=10سم، والضلع (ب ج)= 14سم، والضلع (أد)= 13سم، جد مساحته.^[١٢]
  • الحل:
    • شبه المنحرف هذا فيه كل الأضلاع معلومة دون معرفة الارتفاع؛ لذلك لإيجاد مساحته يمكن استخدام صيغة هيرون: م=((و-أ)(و-ب)(و-أ-ج)(و-أ-د))√×(|أ-ب|)/(أ+ب)، ولاستخدامها يجب أولاً حساب و=2/محيط شبه المنحرف= 2/(13+25+10+14)=31سم.
    • تعويض الأرقام في الصيغة السابقة: م=((و-أ)(و-ب)(و-أ-ج)(و-أ-د))√×(أ+ب)/(|أ-ب|)=((31-25)(31-10)(31-25-14)(31-25-13))√×(10+25)/(|10-25|)=((6)(21)(8-)(7-)√2.333=84×2.333=196سم² تقريباً.

لمزيد من المعلومات والامثلة حول محيط شبه المنحرف يمكنك قراءة المقال الآتي: قانون محيط شبه المنحرف.
لمزيد من المعلومات والامثلة حول محيط شبه المنحرف القائم يمكنك قراءة المقال الآتي: محيط شبه المنحرف القائم.

فيديو عن شبه المنحرف خصائصه ومساحته

للتعرف حول المزيد شاهد الفيديو:^[١٣]

المراجع

1. ↑ “Area Formulas for Geometric Figures”, onlinemschool.com, Retrieved 23-2-2020. Edited.
2. ↑ “Trapezoid”, www.mathsisfun.com, Retrieved 23-2-2020. Edited.
3. ↑ Matthew Perdue (25-4-2017), “How to Find the Area of a Trapezoid Without the Length of One of the Parallel Sides”، www.sciencing.com, Retrieved 14-2-2019. Edited.
4. ↑ “Trapezoid”, www.mathsisfun.com, Retrieved 22-12-2017. Edited.
5. ↑ “Area-and-Perimeter-of-Trapezoids”, www.ck12.org, Retrieved 22-12-2017. Edited.
6. ↑ “How To Find the Area of a Trapezoid”, tutors.com, Retrieved 24-2-2020. Edited.
7. ↑ “Area of a Trapezoid”, www.mathgoodies.com, Retrieved 24-2-2020. Edited.
8. ^ ^{أ ب} “Example Questions”, www.varsitytutors.com, Retrieved 24-2-2020. Edited.
9. ^ ^{أ ب ت} “Area of Trapezium”, www.math-only-math.com, Retrieved 24-2-2020. Edited.
10. ↑ “Trapezoid Problems”, www.superprof.co.uk, Retrieved 24-2-2020. Edited.
11. ^ ^{أ ب} “Area of Trapezuim”, www.teachoo.com, Retrieved 24-2-2020. Edited.
12. ↑ “Herons formula”, www.teachoo.com, Retrieved 24-2-2020. Edited.
13. ↑ فيديو عن شبه المنحرف خصائصه ومساحته.