يُمكن تعريف مساحة سطح الكرة (بالإنجليزية: Surface area of a sphere) على أنه مقدار المساحة الإجمالية التي يشغلها سطح الكرة،[١] ولإيجاد مساحة سطح الكرة يتم ضرب العدد (4) بالثابت باي، ثم ضرب الناتج بمربع نصف القطر، أي من خلال تطبيق المعادلة الآتية:[٢]
- مساحة سطح الكرة= 4×π×مربع نصف القطر، وبالرموز: م=4×π×نق²؛ حيث:
- م: مساحة سطح الكرة.
- نق: نصف قطر الكرة.
- π: باي، ثابت عددي قيمته 3.14 أو 22/7.
- فمثلاً لحساب مساحة سطح الكرة التي تبلغ قيمة نصف قطرها 5سم يُمكن تطبيق القانون كما يأتي: تعويض قيمة نصف القطر نق في معادلة مساحة سطح الكرة= 4×π×نق²= 4×3.14×(5)²، لينتج أن مساحة سطح الكرة= 314سم².[٢]
تجدر الإشارة إلى أن قطر الكرة يساوي ضعفي نصف قطرها؛ أي أن: قطر الكرة=2 ×نصف قطر الكرة، وبالرموز: ق=2نق، أو نق=ق/2، وبالتالي يُمكن حساب مساحة سطح الكرة بتعويض قيمة القطر بدلاً من نصف القطر في القانون لينتج من ذلك أن مساحة سطح الكرة= 4×π×(ق/2)²، ثم بتبسيط المعادلة ينتج أن قانون مساحة سطح الكرة باستخدام القطر:[٣]
- مساحة سطح الكرة= مربع القطر×π ، وبالرموز:م=π×ق²؛ حيث:
- م : مساحة سطح الكرة.
- ق: قطرالكرة.
- π: باي، ثابت عددي قيمته 3.14 أو 22/7.
كما يُمكن إعادة ترتيب المعادلة لحساب قيمة نصف القطر وذلك عند معرفة مساحة سطحها باستخدام المعادلة الآتية:[٤]
- نصف القطر=الجذر التربيعي للقيمة (مساحة سطح الكرة/4π)، وبالرموز: نق=(م/4π)√ ؛ حيث:
- م: مساحة سطح الكرة.
- π: باي، ثابت عددي قيمته 3.14 أو 22/7.
- نق: نصف قطر الكرة.
لمزيد من المعلومات والأمثلة حول مساحة الكرة يُمكنك قراءة المقال الآتي: قانون مساحة سطح الكرة.
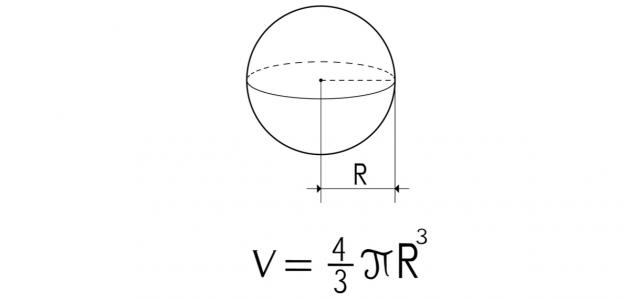
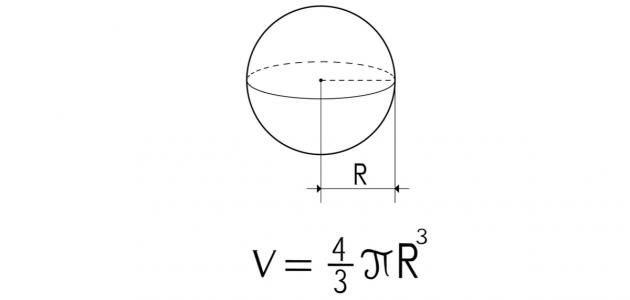
يُمكن تعريف حجم الكرة (بالإنجليزية: Sphere’s Volume) على أنه كمية الفراغ الموجودة داخل الجسم ثلاثي الأبعاد،[٥] ويُقاس بالوحدات المكعّبة، ولإيجاد حجم الكرة يتم ضرب أربعة أثلاث الثابت العددي باي، بمكعب نصف القطر،لتنتج المعادلة الآتية:[٢]
- حجم الكرة=4/3×π×مكعب نصف القطر، وبالرموز: ح=4/3×π×نق³؛ حيث:
- نق: نصف قطر الكرة.
- π: باي، ثابت عددي قيمته 3.14 أو 22/7.
- ح: حجم الكرة.
- ولإيجاد حجم الكرة التي نصف قطرها 3سم يُمكن تطبيق القانون كما يأتي: تعويض قيمة نصف القطر نق في معادلة حجم الكرة= 4/3×π×نق³= 4/3×3.14×(3)³، ومنه حجم الكرة= 113.04سم³.[٢]
لمزيد من المعلومات والأمثلة حول حجم الكرة يُمكنك قراءة المقال الآتي: قانون حجم الكرة في الرياضيات.
- المثال الأول: كرة نصف قطرها 6سم، ما هي مساحة سطحها، وما هو حجمها؟[٦]
- الحل:
- تعويض قيمة نصف القطر نق في معادلة مساحة سطح الكرة= 4×π×نق²= 4×3.14×(6)²، ومنه مساحة سطح الكرة= 452.16سم².
- تعويض قيمة نصف القطر نق في معادلة حجم الكرة= 4/3×π×نق³= 4/3×3.14×(6)³، ومنه حجم الكرة= 904.32 سم³.
- المثال الثاني: نصف قطر مجسم مصغّر للكرة الأرضيّة هو 14سم، ما هي مساحة سطحها، وما هو حجمها؟[٦]
- الحل:
- تعويض قيمة نصف القطر نق في معادلة مساحة سطح الكرة= 4×π×نق²= 4×3.14×(14)²، ومنه مساحة سطح الكرة= 2461.76 سم².
- تعويض قيمة نصف القطر نق في معادلة حجم الكرة= 4/3πنق³= 4/3×3.14×(14)³، ومنه حجم الكرة= 11,488.21سم³.
- المثال الثالث: تضاعف نصف قطر كرة إلى أربعة أضعاف نصف قطرها الأصلي، فإذا كان نصف قطرها الأصلي هو 4سم، فهل ستتضاعف مساحة سطحها أربع مرّات؟[٣]
- الحل:
- تعويض قيمة نصف القطر نق الأصلي في معادلة مساحة سطح الكرة= 4×π×نق²= 4×π×(4)²، ومنه مساحة سطح الكرة الأصلي= 64πسم².
- تعويض قيمة نصف القطر نق المضاعف 4 مرات؛ أي الذي يساوي 4×4=16سم في معادلة مساحة سطح الكرة= 4×π×نق²=4×π×16²، ومنه مساحة سطح الكرة المضاعف 4 مرات = 1024πسم².
- وبقسمة المساحة بعد مضاعفة نصف القطر على المساحة الأصلية ينتج أن: 1024πسم²/ 64πسم²= 16، ومنه فإن المساحة الأصلية قد تضاعفت 16 مرّة مقارنة بمساحة السطح الأصلي، ولم تتضاعف أربع مرّات.
- المثال الرابع: كرة قطرها 4م، ما هو حجمها؟[٣]
- الحل:
- حساب قيمة نصف القطر بقسمة القطر على 2 لينتج أن: نق= ق/2= 4/2= 2م.
- تعويض قيمة نصف القطر نق في معادلة حجم الكرة= 4/3×π×نق³= 4/3×3.14×(2)³، ومنه حجم الكرة= 33.5م³.
- المثال الخامس: كرة حجمها 36π، ما هي مساحتها السطحيّة؟[٧]
- الحل:
- حساب قيمة نصف القطر نق بتعويض قيمة حجم الكرة في قانون حجم الكرة لينتج أن: π36= نق³×4/3×π، ومنه نق= 3سم.
- تعويض قيمة نصف القطر نق في معادلة مساحة سطح الكرة= 4×π×نق²= 4×π×(3)²، ومنه مساحة سطح الكرة= 36πسم².
- المثال السادس: كرة مساحتها السطحية هي 100πسم²، ما هو نصف قطرها؟[٨]
- الحل:
- حساب قيمة نق بتعويض قيمة مساحة الكرة في قانون مساحة سطح الكرة لينتج أن: 100×π×4=π×نق² ، وبقسمة الطرفين على 4π، ينتج أن: 25= نق²، ومنه قيمة نق= 5سم.
- المثال السابع: كرة حجمها 14137.167سم³، ما هو نصف قطرها؟[٨]
- الحل:
- حساب قيمة نق بتعويض قيمة الحجم في قانون حجم الكرة= 4/3×π×نق³=14137.167، ومنه قيمة نق= 15سم.
- المثال الثامن: كرة شاطئ مساحتها السطحيّة 78.54سم²، ما هو نصف قطرها؟[٩]
- الحل:
- حساب قيمة نق بتعويض قيمة مساحة الكرة في قانون مساحة سطح الكرة، لينتج أن: 78.54= 4×π×نق² =4×3.14× نق²، ومنه قيمة نق= 2.5سم.
- المثال التاسع: ما هو حجم كرة الشاطئ السابقة؟[٩]
- الحل:
- تعويض قيمة نصف القطر نق في معادلة حجم الكرة= 4/3×π×نق³= 4/3×3.14×(2.5)³، ومنه حجم الكرة= 65.41 سم³.
- ↑ Sharad_Bhardwaj, “Calculate Volume and Surface area Of Sphere”، www.geeksforgeeks.org, Retrieved 27-3-2020. Edited.
- ^ أ ب ت ث “Finding the Volume and Surface Area of a Sphere”, www.ducksters.com, Retrieved 27-3-2020. Edited.
- ^ أ ب ت “Surface Area and Volume of Spheres”, www.brainfuse.com, Retrieved 27-3-2020. Edited.
- ↑ “Surface area of a sphere”, www.mathopenref.com, Retrieved 27-3-2020. Edited.
- ↑ Yuanxin (Amy) Yang Alcoce, “Spheres: Definition, Area & Volume”، www.study.com, Retrieved 27-3-2020. Edited.
- ^ أ ب “Finding the Volume and Surface Area of a Sphere”, www.courses.lumenlearning.com, Retrieved 27-3-2020. Edited.
- ↑ Worranat Pakornrat, Thaddeus Abiy, Geoff Pilling, and others, “Surface Area of a Sphere”، www.brilliant.org, Retrieved 27-3-2020. Edited.
- ^ أ ب “Surface Area and Volume of Spheres”, www.ck12.org, Retrieved 27-3-2020. Edited.
- ^ أ ب “Spheres – Surface Area & Volume”, www.wrps.org, Retrieved 27-3-2020. Edited.