جديد قانون حجم متوازي المستطيلات

حجم متوازي المستطيلات

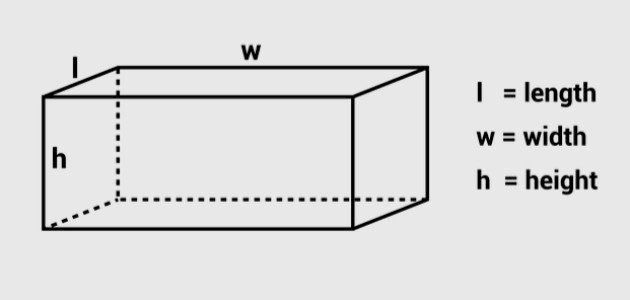
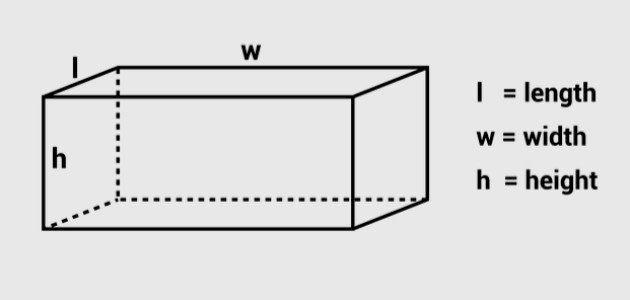
يعرف الحجم بأنه كمية الفراغ أو المادة التي توجد داخل الشكل ثلاثي الأبعاد، ويقاس الحجم بوحدة المتر المكعب وفقاً للنظام العالمي للوحدات،^[١] ويمكن حساب حجم متوازي المستطيلات الذي يعتبر شكلاً ثلاثي الأبعاد من خلال القانون الآتي:^[٢]

• حجم متوازي المستطيلات= الطول×العرض×الارتفاع ، وبالرموز: ح=أ×ب×جـ؛ حيث:
  • ح: حجم متوازي المستطيلات.
  • أ: طول متوازي المستطيلات.
  • ب: عرض متوازي المستطيلات.
  • جـ: ارتفاع متوازي المستطيلات.

لمزيد من المعلومات حول متوازي المستطيلات يمكنك قراءة المقال الآتي: تعريف متوازي المستطيلات.

أمثلة على حساب حجم متوازي المستطيلات

• المثال الأول: ما هو حجم متوازي المستطيلات الذي طوله 14سم، وعرضه 12سم، وارتفاعه 8سم؟^[٣]
  • الحل: حجم متوازي المستطيلات = الطول×العرض×الارتفاع، وبالتالي:
    • حجم متوازي المستطيلات = 14 × 12 × 8 = 1344سم³.

• المثال الثاني: ما هو حجم متوازي الذي طوله 14سم، وعرضه 50مم، وارتفاعه 10سم؟^[٣]
  • الحل: حجم متوازي المستطيلات = الطول×العرض×الارتفاع
  • بما أن الطول، والارتفاع بوحدة السنتيمتر، فإنه يجب تحويل العرض ليصبح بوحدة السنتيمتر، وذلك لتصبح جميع الأبعاد بنفس الوحدة، ومن المعروف أن 10مم = 1سم، وبالتالي فإن العرض يساوي: 50مم / 10سم = 5سم.
  • بعد أن أصبحت الأبعاد بنفس الوحدة، فإن يمكن إيجاد الحجم كما يلي:
    • حجم متوازي المستطيلات = 14×5×10= 700سم³.

• المثال الثالث: ما هي تكلفة شراء قوالب الطوب التي يجب استخدامها لبناء حائط على شكل متوازي مستطيلات طوله 20م، و ارتفاعه 2م، وعرضه 0.75 م، علما أن كل قالب طوب ارتفاعه 7.5 سم، وطوله 25سم، وعرضه 10سم، وأن كل 1000 قالب من الطوب قيمته 900 عملة نقدية؟^[٣]
  • الحل:
  • حجم الحائط يمثل حجم متوازي المستطيلات، ويمكن حسابه كما يلي:
    • حجم الحائط = الطول×العرض×الارتفاع= 20م × 2م × 0.75م=30م³.
  • حجم قوالب الطوب يمثل أيضاً حجم متوازي المستطيلات، ويمكن حسابه كما يلي:
    • حجم قالب الطوب = 25سم×10سم×7.5سم =1875سم³.
  • عدد قوالب الطوب المطلوبة= حجم الحائط / حجم قوالب الطوب، إلا أن حجم قوالب الطوب مقاس بالسنتيمتر المكعب، أما حجم الحائط فمُقاس بالمتر المكعب؛ لذلك يجب توحيد الوحدات عن طريق تحول حجم الحائط إلى السنتيمتر المكعب بقسمة الحجم على القيمة (1,000,000)؛ لأن كل 1م³=1,000,000سم³، ومنه: حجم قالب الطوب بالمتر المكعب= 1875/1,000,000= 0.001875م³.
    • عدد قوالب الطوب = 30/0.001875= 16,000 قالب من الطوب.
  • إجراء عملية النسبة، والتناسب بين عدد القوالب، وتكلفتها كما يلي:
    • كل 1000 قالب ← تكلفته 900 عملة نقدية
    • كل 16,000 قالب ← ؟؟
    • بإجراء عملية الضرب التبادلي فإن تكلفة القوالب = 900×16,000/ 1,000، ويساوي 14,400 عملة نقدية.

• المثال الرابع: بركة سباحة للألعاب الأولمبية طولها 50م، وعرضها 25م، وعمق المياه فيها 2م، فما هي كمية المياه التي تتسع لها هذه البركة؟^[٤]
  • الحل:
    • يمكن التعبير عن كمية المياه في هذه البركة باستخدام الحجم، وحجم المياه يساوي حجم متوازي المستطيلات، ويمكن إيجاده كما يلي:
    • حجم متوازي المستطيلات = الطول×العرض×الارتفاع= 50×25×2= 2500 م³، وهو كمية الماء الموجودة في هذه البركة.

• المثال الخامس: إذا كان طول متوازي المستطيلات 8سم، وارتفاعه 3سم، فما هو عرضه علماً أن حجمه 120سم³؟^[٤]
  • الحل:
    • حجم متوازي المستطيلات = الطول×العرض×الارتفاع، ومنه:
    • 120 = 8×العرض×3
    • بحل هذه المعادلة فإن العرض = 5سم.

• المثال السادس: صمّم فؤاد صندوقاً على شكل متوازي مستطيلات حجمه 2500سم³، وارتفاعه 25سم، وقاعدته مربعة الشكل، ثم أدرك أنه يحتاج إلى صندوق أصغر حجماً فقصّ من ارتفاعه ليصبح حجمه 1000سم³، وبقيت مساحة قاعدته كما هي، فكم أصبح ارتفاعه، وهل أصبح شكل الصندوق مكعباً؟^[١]
  • الحل:
  • حساب مساحة القاعدة باستخدام قانون حجم متوازي المستطيلات = الطول × العرض × الارتفاع.
    • بما أن الحجم = 2500سم³، والارتفاع = 25سم، وبتعويض هذه القيم في قانون الحجم يمكن الحصول على مساحة القاعدة مربعة الشكل كما يلي:.
    • 2500 = (الطول×العرض)×الارتفاع= (الطول×العرض)×25، وبقسمة الطرفين على (25) ينتج أن: 100 سم²= الطول×العرض، وهي تمثل مساحة القاعدة.
  • حساب طول، وعرض القاعدة مربعة الشكل كما يلي:
    • مساحة القاعدة = (طول الضلع)²، ومنه: طول الضلع = 100√= 10سم، وبما أن القاعدة مربعة الشكل فإن عرضها يساوي 10سم أيضاً.
  • حساب ارتفاع الصندوق بعد قص جزء من ارتفاعه عن طريق قانون حجم متوازي المستطيلات، لينتج أن: حجم الصندوق بعد القص = الطول×العرض×الارتفاع، ومنه:
    • 1000 = 10×10×الارتفاع، وبقسمة الطرفين على (100) ينتج أن: الارتفاع الجديد = 10سم.
  • بما أن الطول = العرض = الارتفاع فإن الشكل الناتج هو مكعب.

• المثال السابع: ما هي كمية الهواء التي توجد داخل غرفة على شكل متوازي مستطيلات طولها يساوي 5م، وعرضها 6م، وارتفاعها 10م؟^[٥]
  • الحل: كمية الهواء داخل الغرفة = سعة الغرفة = حجم متوازي المستطيلات.
  • حجم متوازي المستطيلات = الطول×العرض×الارتفاع
  • حجم متوازي المستطيلات = 5×6×10= 300م³، وبالتالي فإن كمية الهواء التي توجد داخل الغرفة 300 م³.

• المثال الثامن: قضيب معدني على شكل متوازي مستطيلات طوله 10م، وعرضه 60سم، وسمكه 25سم، فما هو ثمنه إذا كانت ثمن المتر المكعب الواحد 250 دولاراً؟^[٦]
  • الحل: لحساب ثمن القضيب المعدني يجب أولاً حساب حجمه؛ لأن الثمن= تكلفة المتر المكعب × حجم متوازي المستطيلات، ومنه:
  • حجم متوازي المستطيلات = الطول×العرض×الارتفاع = 10×(60/100)×(25/10)، وتجدر الإشارة أنه تم القسمة على 100 للتحويل من سم إلى متر.
  • حجم متوازي المستطيلات = 1.5م³.
  • ثمن القضيب المعدني= 1.5×250 = 375 دولاراً.

• المثال التاسع: ما هو ارتفاع متوازي المستطيلات علماً أن حجمه 300سم³، ومساحة قاعدته 30سم؟^[٦]
  • الحل: حجم متوازي المستطيلات = الطول × العرض × الارتفاع، ويمكن إيجاد الارتفاع كما يلي:
    • القاعدة تكون على شكل مستطيل، وبالتالي فإن مساحتها = الطول×العرض، وتساوي 30سم.
    • يمكن إيجاد الارتفاع من قانون الحجم كما يلي: 300 = 30×الارتفاع ، ومنه:
    • الارتفاع = 300/30 = 10سم.

• المثال العاشر: بركة سباحة فارغة على شكل متوازي مستطيلات طولها 25م، وعرضها 10م، وعمقها 2م، يمكن تعبئتها بالماء بمعدل 800 لتر لكل دقيقة فكم من الوقت بالدقائق، والساعات يلزم لتعبئتها كاملة علماً أن كل متر مكعب = 1000لتر؟^[٧]
  • الحل:
  • حساب كمية الماء اللازمة لملء البركة، والتي يمكن حسابها باستخدام قانون حجم متوازي المستطيلات = الطول×العرض×الارتفاع، ومنه:
    • حجم متوازي المستطيلات = 25×10×2= 500م³، وهي كمية الماء اللازمة لملء البركة بالماء.
  • الوقت الذي يلزم لتعبئتها كاملة = الحجم / معدل التعبئة، إلا أنه يجب أولاً تحويل معدل التعبئة من الليتر إلى المتر المكعب، وذلك بقسمته على (1000)؛ لأن كل متر مكعب = 1000لتر؛ أي أن 800 لتر/ دقيقة=800/1000= 0.8م³ /دقيقة، وبالتالي:
    • الوقت اللازم لتعبئة البركة كاملة = 500م³/ ((0.8)م³/دقيقة)، ومنه الوقت بالدقائق= 625 دقيقة، أما الوقت بالساعات = 625 /60 = 10ساعات ونصف تقريباً

• المثال الحادي عشر: صندوقان أ، وب على شكل متوازي مستطيلات فإذا كانت أبعاد (أي الطول، والعرض) قاعدة الصندوق أ: 10سم × 8سم، وأبعاد قاعدة الصندوق ب: 15سم × 10سم، فإذا تم تعبئة الصندوق أ بالمياه فوصل إلى ارتفاع 15سم، ثم تم سكب هذه المياه في الصندوق (ب) فإلى أي ارتفاع سيصل ارتفاع المياه في هذا الصندوق؟^[٨]
  • الحل:
    • كمية (حجم) المياه في الصندوق أ = كمية (حجم) المياه في الصندوق ب، وبالتعويض في قانون حجم متوازي المستطيلات= الطول × العرض × الارتفاع، ينتج أن:
    • 10×8×15 = 15×10×الارتفاع، وبحل المعادلة ينتج أن: الارتفاع = 8سم.

• المثال الثاني عشر: إذا كان حجم صندوق على شكل متوازي مستطيلات 1440م³، وطوله 15م، وارتفاعه 8م، فما هو ارتفاعه؟^[٩]
  • الحل:
  • حجم متوازي المستطيل = الطول×العرض×الارتفاع، ومنه:
  • 1440= 15×8×الارتفاع، وبحل المعادلة ينتج أن: الارتفاع= 1440/120= 12م.

• المثال الثالث عشر: إذا كانت أبعاد قاعدة صندوق على شكل متوازي مستطيلات 80سم×40سم، وكان حجمه 160 لتر، وأراد أحمد طلاء جميع جوانب الصندوق باستثناء قاعدته السفلية، وكانت تكلفة الطلاء 6000 عملة نقدية/م²، جد تكلفة طلاء هذا الصندوق.^[٨]
  • الحل:
  • حساب ارتفاع الصندوق باستخدام قانون حجم متوازي المستطيلات، إلا أنه يجب أولاً تحويل الليتر إلى سنتيمتر مكعب لتوحيد الوحدات عن طريق ضرب الحجم بالقيمة (1,000)؛ لأن 1ليتر=1,000سم³ لينتج أن: حجم متوازي المستطيل=160ليتر= 160,000سم³، وبتعويض القيمة في قانون حجم متوازي المستطيلات: الطول×العرض×الارتفاع، لينتج أن:
    • 160,000=80×40×الارتفاع، ومنه: الارتفاع= 50سم.
  • حساب مساحة الصندوق باستثناء قاعدته السفلية لحساب تكلفة طلائه:
    • مساحة متوازي المستطيلات باستثناء قاعدته السفلية=المساحة الجانبية+مساحة القاعدة العلوية=2 ×الارتفاع×(الطول+العرض)+الطول×العرض=2 ×50×(80+40)+80×40=15,200سم²=1.52م²؛ لأن كل 1م²=1000سم².
  • حساب تكلفة الطلاء= مساحة الصندوق × تكلفة الطلاء= 1.52م²× 6000 عملة نقدية/م²= 9,120 عملة نقدية.

لمزيد من المعلومات حول مساحة متوازي المستطيلات يمكنك قراءة المقال الآتي: قانون مساحة متوازي المستطيلات.

فيديو عن حجم ومساحة متوازي المستطيلات

للتعرف على هذا الشكل الهندسي تابع الفيديو:^[١٠]

المراجع

1. ^ ^{أ ب} “Cube and Cuboid”, www.toppr.com, Retrieved 5-4-2020. Edited.
2. ↑ “Volume of a Cuboid”, www.mathsisfun.com, Retrieved 5-4-2020. Edited.
3. ^ ^{أ ب ت} “Cuboid”, www.math-only-math.com, Retrieved 5-4-2020. Edited.
4. ^ ^{أ ب} “Volume of a Cuboid “, www.mathopolis.com, Retrieved 5-4-2020. Edited.
5. ↑ “Volume Of Cuboid”, byjus.com, Retrieved 5-4-2020. Edited.
6. ^ ^{أ ب} “Volume of a Cuboid”, www.web-formulas.com, Retrieved 5-4-2020. Edited.
7. ↑ “Volume of a Cuboid”, corbettmaths.com, Retrieved 5-4-2020 (page 3). Edited.
8. ^ ^{أ ب} “Volume of a cuboid”, www.cuemath.com, Retrieved 5-4-2020. Edited.
9. ↑ “VOLUME OF CUBOID WORD PROBLEMS”, www.onlinemath4all.com, Retrieved 5-4-2020. Edited.
10. ↑ فيديو عن حجم ومساحة متوازي المستطيلات.