ارتفاع مثلث متساوي الساقين

• ذات صلة
• خصائص المثلث متساوي الساقين
• كيف أحسب ارتفاع المثلث

سُمّي المثلث متساوي الساقين بهذا الاسم لاحتوائه على ضلعين متساويين في الطول، كما تكون زوايا قاعدته متساوية أيضاً، ويمكن قياس ارتفاع المثلث متساوي الساقين (بالإنجليزية: Height) الذي يُعرف بأنه القطعة المستقيمة الواصلة بين رأس المثلث وقاعدته، وتكون عمودية على القاعدة، باستخدام عدة قوانين رياضية، مثل: قانون مساحة المثلث، ونظرية فيثاغورس، وقانون هيرون، وذلك كما يأتي.^[١]

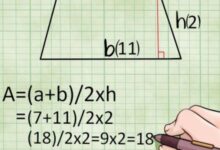
يمكن حساب ارتفاع المثلث بواسطة قانون مساحة المثلث إذا عُلِمت مساحته وطول قاعدته، حيث إنّ:^[١]

• مساحة المثلث= ½ × طول القاعدة × الارتفاع، وبترتيب المعادلة ينتج أن: ارتفاع المثلث=(2×مساحة المثلث)/طول قاعدة المثلث؛ وبالرموز: ع=(2×م)/ق؛ حيث:
  • ع: ارتفاع المثلث.
  • م: مساحة المثلث.
  • ق: قاعدة المثلث.

فمثلاً لو كان هناك مثلث طول قاعدته 20 سم، ومساحته 120سم²، فإن ارتفاعه من العلاقة السابقة وبتعويض القيم فيها هو:

• 120= ½×20×الارتفاع، وبحل المعادلة ينتج أن الارتفاع=12سم.

تختص نظرية فيثاغورس بالمثلث قائم الزاوية، ويمكن استخدامها لمعرفة أطوال أضلاع المثلث متساوي الساقين إذا عُلم طول قاعدته، وطول أحد ضلعيه المتساويين، وذلك عن طريق اتباع الخطوات الآتية:^[٢]

• إسقاط عمود من رأس المثلث متساوي الساقين على قاعدته، لتنصيف قاعدته والحصول على مثلثين قائمي الزاوية ومتطابقين.
• اعتبار أن طول أحد ساقي المثلث هو طول الوتر.
• اعتبار أن طول قاعدة المثلث قائم الزاوية هو طول نصف قاعدة المثلث متساوي الساقين.
  • تطبيق قانون نظرية فيثاغورس، وهو: (الوتر أو طول أحد ساقي المثلث المتساويتين)²= (طول نصف القاعدة)²+ (الارتفاع)²، وبترتيب المعادلة يمكن الحصول على القانون الآتي: الارتفاع=الجذر التربيعي لـ (مربع طول الساق-مربع طول القاعدة/4)، وبالرموز: ع= (أ²-ب²/ 4)√؛ حيث:^[٣]
  • ع: ارتفاع المثلث.
  • أ: طول إحدى ساقي المثلث متساوي الساقين.
  • ب: طول القاعدة.

فمثلاً لحساب ارتفاع مثلث متساوي الساقين طول قاعدته 12سم، وطول أحد ساقيه المتساويتين 20سم يجب التعويض بالقيم المُعطاه في قانون نظرية فيثاغورس لينتج أن:

• 20²=6²+الارتفاع²، ومنه الارتفاع=19سم
• أو التعريض في الصيغة: ع= (أ²-ب²/ 4)√، لينتج أن ع= (20²-12²/ 4)√= 19سم.^[٤]

يُمكن حساب مساحة المثلث بواسطة صيغة هيرون (بالإنجليزية: Heron’s Formula) إذا عُلِمت أطوال أضلاعه الثلاثة، وبعد حساب قيمة المساحة يمكن استخدامها وتعويضها في قانون مساحة المثلث لمعرفة ارتفاعه.^[٥] وقانون مساحة المثلث وفق صيغة هيرون هو: مساحة المثلث= (س(س-أ)×(س-ب)×(س-ج))√؛ حيث إنّ:

• س: قيمة منتصف محيط المثلث؛ أي مجموع أطوال أضلاع المثلث مقسوماً على 2، وبالرموز: س=(أ+ب+ج/2).
• أ: طول الضلع الأول.
• ب: طول الضلع الثاني.
• ج: طول الضلع الثالث.

فمثلاً لحساب ارتفاع مثلث متساوي الساقين طول قاعدته 12سم، وطول أحد ساقيه المتساويتين 20سم، يمكن التعويض في الصيغة السابقة لينتج أن:

• س=(أ+ب+ج/2)=(12+20+20)/2=26سم
• مساحة المثلث=(س×(س-أ)×(س-ب)×(س-ج))√=(26×(26-12)×(26-20)×(26-20))√=114.5سم².
• حساب ارتفاع المثلث من خلال التعويض في قانون المساحة: ع=(2×م)/ق=(2×114.5)/12=19سم.

• المثال الأول: إذا كان طول قاعدة مثلث متساوي الساقين 12سم، ومساحته 42سم²، جد ارتفاعه.^[٦]

الحل:

• باستخدام القانون: ع=(2×م)/ق، ومنه ع=(2×42)/12=7سم.

• المثال الثاني: إذا كان طول محيط مثلث متساوي الساقين 22سم، وكان طول قاعدته يقل بمقدار 2سم عن ضعفي طول إحدى ساقيه، جد ارتفاعه.^[٦]

الحل:

• نفترض أن طول ساقي المثلث= س، وطول القاعدة= 2س-2، ثم وباستخدام القانون:
• محيط المثلث متساوي الساقين= 2×طول إحدى الساقين+ طول القاعدة، ينتج أن: 22=2س+2س-2، ومنه س=6سم؛ أي أن طول ساقي المثلث=6سم، وطول قاعدته=2س-2=2(6)-2=10سم.
• باستخدام قانون فيثاغورس، ينتج أن:
• (الوتر أو طول أحد ساقي المثلث المتساويتين)²= (طول نصف القاعدة)²+ (الارتفاع)²، 6²=5²+(الارتفاع)²، ومنه الارتفاع=3.32سم.

• المثال الثالث: إذا كان طول محيط مثلث متساوي الساقين 32سم، وكان طول قاعدته يقل بمقدار 18سم عن ثلاثة أضعاف طول إحدى ساقيه، جد ارتفاعه.^[٦]

الحل:

• نفترض أن طول ساقي المثلث= س، وطول القاعدة= 3س-18
• باستخدام القانون: محيط المثلث متساوي الساقين= 2×طول إحدى الساقين+ طول القاعدة، ينتج أن:
• 32=2س+3س-18، ومنه س=10سم؛ أي أن طول ساقي المثلث=10سم، وطول قاعدته=3س-18=3(10)-18=12سم.
• حساب قيمة س لاستخدام صيغة هيرون لينتج أن: س=(أ+ب+ج/2)، س=(12+10+10)/2=16، ثم تعويض القيم في قانون هيرون، لينتج أن:
• مساحة المثلث= (س(س-أ)×(س-ب)×(س-ج))√= (16(16-10)×(16-10)×(16-12))√=48سم².
• حساب الارتفاع باستخدام القانون: ع=(2×م)/ ق
• لينتج أن: ع=(2×48)/12=8سم.

• المثال الرابع: إذا كان محيط مثلث متساوي الساقين 42سم، وطول قاعدته يعادل 3/2ضعف كل ساق من ساقيه، جد ارتفاع هذا المثلث.^[٧]

الحل:

• نفترض أن طول ساقي المثلث= س، وطول القاعدة=3/2س، ثم وباستخدام القانون:
• محيط المثلث متساوي الساقين= 2×طول إحدى الساقين+ طول القاعدة
• 42=2س+3/2س، ومنه س=12سم؛ أي أن طول ساقي المثلث=12سم، وطول قاعدته=3/2س=18سم.
• باستخدام قانون فيثاغورس: (الوتر أو طول أحد ساقي المثلث المتساويتين)²= (طول نصف القاعدة)²+ (الارتفاع)²
• 12²=9²+(الارتفاع)²، ومنه الارتفاع=7.93سم.

1. ^ ^{أ ب} “Triangles”, mathsisfun.com, Retrieved 11-4-2019. Edited.
2. ↑ Stephen La Rocque, ” finding the height of a triangle”، mathcentral.uregina.ca, Retrieved 11-4-2019. Edited.
3. ↑ “ISOSCELES TRIANGLE”, www.mathematicalway.com, Retrieved 23-3-2020. Edited.
4. ↑ smendyka (22-2-2018), “An isosceles triangle has a base of 12 cm with equal sides of 20 cm each. How do you determine the area of this triangle accurate to the nearest square centimeter?”، socratic.org, Retrieved 11-4-2019. Edited.
5. ↑ “Heron’s Formula”, www.mathsisfun.com, Retrieved 11-4-2019. Edited.
6. ^ ^{أ ب ت} “Example Questions”, www.varsitytutors.com, Retrieved 23-3-2020. Edited.
7. ↑ “The perimeter of an isosceles triangle”, www.toppr.com, Retrieved 23-3-2020. Edited.